题目内容
已知blnb+b-2=0,求b.
考点:函数的零点
专题:函数的性质及应用,导数的综合应用
分析:求导数得出f′(x)=lnx+2,判断出f(x)=xlnx+x-2,在(0,
)单调递减,(
,+∞)单调递增.,=
时,f(x)极小值=f(
)=-
-4<0,根据根的范围问题求解得出(x)=xlnx+x-2有一个零点x0,x0∈(1,2),即可得出b 范围.
| 1 |
| e2 |
| 1 |
| e2 |
| 1 |
| e2 |
| 1 |
| e2 |
| 2 |
| e2 |
解答:
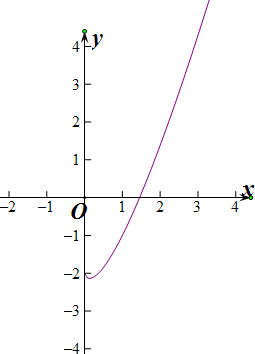 解:∵f(x)=xlnx+x-2,
解:∵f(x)=xlnx+x-2,
∴f′(x)=lnx+2,
∵f′(x)=lnx+2=0,x=
,
f′(x)=lnx+2<0,0<x<
f′(x)=lnx+2>0,x>
,
∴f(x)=xlnx+x-2,在(0,
)单调递减,(
,+∞)单调递增.
x=
时,f(x)极小值=f(
)=-
-4<0,
当x→0,f(x)→-2,
f(1)=-1<0,
f(2)=2ln2>0,
∴f(x)=xlnx+x-2有一个零点x0,x0∈(1,2)
∴方程blnb+b-2=0,有1个根,b∈(1,2)
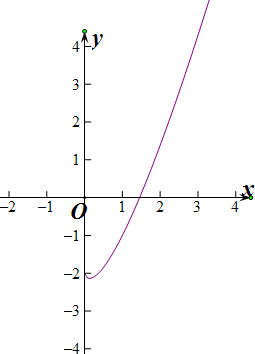 解:∵f(x)=xlnx+x-2,
解:∵f(x)=xlnx+x-2,∴f′(x)=lnx+2,
∵f′(x)=lnx+2=0,x=
| 1 |
| e2 |
f′(x)=lnx+2<0,0<x<
| 1 |
| e2 |
f′(x)=lnx+2>0,x>
| 1 |
| e2 |
∴f(x)=xlnx+x-2,在(0,
| 1 |
| e2 |
| 1 |
| e2 |
x=
| 1 |
| e2 |
| 1 |
| e2 |
| 2 |
| e2 |
当x→0,f(x)→-2,
f(1)=-1<0,
f(2)=2ln2>0,
∴f(x)=xlnx+x-2有一个零点x0,x0∈(1,2)
∴方程blnb+b-2=0,有1个根,b∈(1,2)
点评:本题综合考查了函数的性质,运用导数与单调性的关系,判断方程的根,函数的零点的问题,属于中档题.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
已知命题P:复数z=1-i在复平面内对应的点位于第四象限;命题q:?x0>0,使x0=cosx0,则下列命题中为真命题的是( )
| A、(¬p)∧(¬q) |
| B、(¬p)∧q |
| C、p∧(¬q) |
| D、p∧q |