题目内容
已知不等式|2x+y-m|＜3表示的平面区域包含点（0，0）和点（-1，1），求实数m的取值范围．
考点：简单线性规划
专题：不等式的解法及应用
分析：已知两点在不等式表示的平面区域内，即两点是不等式的解，分别代入解不等式即可得m的取值范围
解答：
解：∵不等式|2x+y+m|＜3表示的平面区域包含点（0，0）和点（-1，1），
∴
解得：-3＜m＜2
∴m的取值范围是（-3，2）
故答案为：（-3，2 ）
∴
|
∴m的取值范围是（-3，2）
故答案为：（-3，2 ）
点评：本题主要考查了二元一次不等式表示平面区域的知识，点与平面区域间的关系，属中档题．
练习册系列答案
阅读快车系列答案
相关题目
已知命题P：复数z=1-i在复平面内对应的点位于第四象限；命题q：?x0＞0，使x0=cosx0，则下列命题中为真命题的是（ ）
| A、（￢p）∧（￢q） |
| B、（￢p）∧q |
| C、p∧（￢q） |
| D、p∧q |
组合式
-2
+4
-8
+…+（-2）n
的值等于（ ）
| C | 0 n |
| C | 1 n |
| C | 2 n |
| C | 3 n |
| C | n n |
| A、（-1）n |
| B、1 |
| C、3n |
| D、3n-1 |
定义在实数集R上的函数y=f（x）的图象是连续不断的，若对任意的实数x，存在不为0的常数r使得f（x+r）=-rf（x）恒成立，则称f（x）是一个“关于r函数”，下列“关于r函数”的结论正确的是（ ）
| A、f（x）=0是常数函数中唯一一个“关于r函数” | ||
| B、f（x）=x2是一个“关于r函数” | ||
| C、f（x）=sinπx不是一个“关于r函数” | ||
D、“关于
|
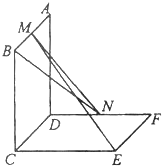如图，已知两个正方形ABCD 和DCEF不在同一平面内，且平面ABCD⊥平面DCEF，M，N分别为AB，DF的中点．