题目内容
若△ABC 的三边长分别为a,b,c,面积为s.则△ABC的内切圆半径 r=
;类似的,若四面体ABCD的四个面的面积分别为s1,s2,s3,s4,体积为V,则四面体ABCD的内切球半径r为( )
| 2s |
| a+b+c |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:类比推理
专题:推理和证明
分析:根据平面与空间之间的类比推理,由点类比点或直线,由直线 类比 直线或平面,由内切圆类比内切球,由平面图形面积类比立体图形的体积,结合求三角形的面积的方法类比求四面体的体积即可.
解答:
 解:由线段长度类比面积,面积类比到体积,即一维类比到二维,二维到三维,
解:由线段长度类比面积,面积类比到体积,即一维类比到二维,二维到三维,
若△ABC 的三边长分别为a,b,c,面积为s.则△ABC的内切圆半径 r=
;类似的,若四面体ABCD的四个面的面积分别为s1,s2,s3,s4,体积为V,则四面体ABCD的内切球半径r为
.
证明如下:
设四面体的内切球的球心为O,
则球心O到四个面的距离都是R,
所以四面体的体积等于以O为顶点,
分别以四个面为底面的4个三棱锥体积的和.
则四面体的体积为 V四面体A-BCD=
(S1+S2+S3+S4)r,
∴r=
故选:B.
 解:由线段长度类比面积,面积类比到体积,即一维类比到二维,二维到三维,
解:由线段长度类比面积,面积类比到体积,即一维类比到二维,二维到三维,若△ABC 的三边长分别为a,b,c,面积为s.则△ABC的内切圆半径 r=
| 2s |
| a+b+c |
| 3v |
| s1+s2+s3+s4 |
证明如下:
设四面体的内切球的球心为O,
则球心O到四个面的距离都是R,
所以四面体的体积等于以O为顶点,
分别以四个面为底面的4个三棱锥体积的和.
则四面体的体积为 V四面体A-BCD=
| 1 |
| 3 |
∴r=
| 3v |
| s1+s2+s3+s4 |
故选:B.
点评:类比推理是指依据两类数学对象的相似性,将已知的一类数学对象的性质类比迁移到另一类数学对象上去.一般步骤:①找出两类事物之间的相似性或者一致性.②用一类事物的性质去推测另一类事物的性质,得出一个明确的命题(或猜想).

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
下面结论中错误的个数为( )
①若f(x)=1,则f′(x)=1
②若f(x)=
,则f′(x)=
③若f(x)=3x,则f′(x)=3
④若f(x)=
,则f′(x)=-
.
①若f(x)=1,则f′(x)=1
②若f(x)=
| x |
| 1 | ||
2
|
③若f(x)=3x,则f′(x)=3
④若f(x)=
| 1 | ||
|
| 1 | ||
2
|
| A、4个 | B、3个 | C、2个 | D、1个 |
已知f(x)=|x-1|,求f(3)=( )
| A、1 | B、2 | C、3 | D、4 |
函数y=x2cos2x的导数为( )
| A、y′=2xcos2x-x2sin2x |
| B、y′=2xcos2x-2x2sin2x |
| C、y′=x2cos2x-2xsin2x |
| D、y′=2xcos2x+2x2sin2x |
在边长为3的正方形ABCD内随机取一点,取到的点到顶点A的距离大于1的概率是( )
A、
| ||
B、1-
| ||
C、
| ||
D、1-
|
已知四面体P-ABC,PA⊥平面ABC,若PA=2,AB=BC=AC=
,则该四面体的外接球的体积为( )
| 6 |
A、
| ||
| B、2π | ||
C、2
| ||
D、4
|
给定两个命题p和q,若p是¬q的充分而不必要条件,则¬p是q的( )
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
 如图,在圆心角为直角的扇形OAB中,随机投入一点,则该点落入三角形区域(阴影部分)的概率为( )
如图,在圆心角为直角的扇形OAB中,随机投入一点,则该点落入三角形区域(阴影部分)的概率为( )A、
| ||
B、
| ||
C、
| ||
D、
|
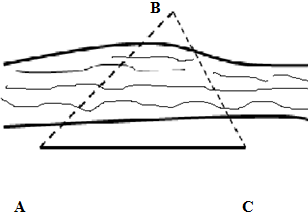 如图,在一次测量活动中,要测量河两岸B、C两点间的距离,测量者在河的一侧,测得AC=24m,∠BAC=45°,∠ACB=75°,求B、C两点间的距离.
如图,在一次测量活动中,要测量河两岸B、C两点间的距离,测量者在河的一侧,测得AC=24m,∠BAC=45°,∠ACB=75°,求B、C两点间的距离.