题目内容
在边长为3的正方形ABCD内随机取一点，取到的点到顶点A的距离大于1的概率是（ ）
A、
| ||
B、1-
| ||
C、
| ||
D、1-
|
考点：几何概型
专题：概率与统计
分析：根据几何概型的概率公式，计算相应的面积即可得到结论．
解答：
解：在正方形ABCD内随机取一点P，点P到点O的距离大于1的轨迹是以O为圆心，1为半径的
圆的外部，面积为32-
×π×12=9-
，
∵正方形的面积为3×3=9，
∴点P到点O的距离大于1的概率为
=1-
．
故选：B．
| 1 |
| 4 |
| 1 |
| 4 |
| π |
| 4 |
∵正方形的面积为3×3=9，
∴点P到点O的距离大于1的概率为
9-
| ||
| 9 |
| π |
| 36 |
故选：B．
点评：本题考查的知识点是几何概型，关键是要找出点到O的距离大于1的点对应的图形的面积，利用数形结合是解决本题的关键．
练习册系列答案
春雨教育同步作文系列答案
相关题目
已知A（-2，-3），B（2，1），C（1，4），D（-7，-4），则有（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
函数y=2cos2x+6sinx+1的最大值为（ ）
| A、10 | B、9 | C、8 | D、7 |
已知y=f（x）是偶函数，而y=f（x+1）是奇函数，且对任意0≤x≤1，都有f′（x）≥0，则a=f（
），b=f（
），c=f（
）的大小关系是（ ）
| 98 |
| 19 |
| 101 |
| 17 |
| 106 |
| 15 |
| A、c＜b＜a |
| B、c＜a＜b |
| C、a＜c＜b |
| D、a＜b＜c |
不等式x2-2x-3＜0的解集为（ ）
| A、{x|x＜-3或x＞1} |
| B、{x|-3＜x＜1} |
| C、{x|x＜-1或x＞3} |
| D、{x|-1＜x＜3} |
若△ABC 的三边长分别为a，b，c，面积为s．则△ABC的内切圆半径 r=
；类似的，若四面体ABCD的四个面的面积分别为s1，s2，s3，s4，体积为V，则四面体ABCD的内切球半径r为（ ）
| 2s |
| a+b+c |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知集合M={x|-1＜x≤1}，N={x|1≤2x＜4}，则M∩N（ ）
| A、{x|-1＜x＜1} |
| B、{x|0≤x＜1} |
| C、{x|0≤x≤1} |
| D、{x|-1＜x＜2} |
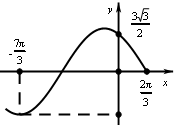已知ω＞0，-π＜φ＜π，函数f（x）=Asin（ωx+φ）的部分图象如图所示，则f（x）解析式为（ ）A、f（x）=3sin（
| ||||
B、f（x）=3sin（
| ||||
C、f（x）=3sin（
| ||||
D、f（x）=3sin（2x+
|
某英语学习小组共12名同学进行英语听力测试，随机抽取6名同学的测试成绩（单位：分），用茎叶图记录如下，其中茎为十位数，叶为个位数．