题目内容
给定两个命题p和q，若p是￢q的充分而不必要条件，则￢p是q的（ ）
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
考点：必要条件、充分条件与充要条件的判断,命题的否定
专题：简易逻辑
分析：根据逆否命题的等价性即可得到结论．
解答：
解：∵p是￢q的充分而不必要条件，
∴根据逆否命题的等价性可知q是￢p的充分而不必要条件，
即￢p是q的必要不充分条件，
故选：B
∴根据逆否命题的等价性可知q是￢p的充分而不必要条件，
即￢p是q的必要不充分条件，
故选：B
点评：本题主要考查充分条件和必要条件的判断，根据逆否命题的等价性是解决本题的关键．
练习册系列答案
相关题目
已知y=f（x）是偶函数，而y=f（x+1）是奇函数，且对任意0≤x≤1，都有f′（x）≥0，则a=f（
），b=f（
），c=f（
）的大小关系是（ ）
| 98 |
| 19 |
| 101 |
| 17 |
| 106 |
| 15 |
| A、c＜b＜a |
| B、c＜a＜b |
| C、a＜c＜b |
| D、a＜b＜c |
若△ABC 的三边长分别为a，b，c，面积为s．则△ABC的内切圆半径 r=
；类似的，若四面体ABCD的四个面的面积分别为s1，s2，s3，s4，体积为V，则四面体ABCD的内切球半径r为（ ）
| 2s |
| a+b+c |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知集合M={x|-1＜x≤1}，N={x|1≤2x＜4}，则M∩N（ ）
| A、{x|-1＜x＜1} |
| B、{x|0≤x＜1} |
| C、{x|0≤x≤1} |
| D、{x|-1＜x＜2} |
已知|
|=3，|
|=4且向量
与
的夹角是
，则向量
在
方向上的投影是（ ）
| a |
| b |
| a |
| b |
| π |
| 6 |
| a |
| b |
A、-
| ||||
B、
| ||||
C、-
| ||||
D、
|
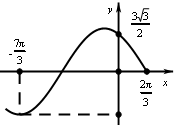已知ω＞0，-π＜φ＜π，函数f（x）=Asin（ωx+φ）的部分图象如图所示，则f（x）解析式为（ ）A、f（x）=3sin（
| ||||
B、f（x）=3sin（
| ||||
C、f（x）=3sin（
| ||||
D、f（x）=3sin（2x+
|