题目内容
16．已知点A，B为圆C：x2+y2=4上的任意两点，且|AB|＞2，若线段AB中点组成的区域为M，在圆C内任取一点，则该点落在区域M内的概率为$\frac{3}{4}$．分析 由题意，求出线段AB中点组成的区域为M为半径为$\sqrt{3}$的同心圆，利用几何概型的公式得到所求．
解答 解：由题意，线段AB中点组成的区域M为以原点为圆心，$\sqrt{3}$为半径的圆，由几何概型的公式得到$\frac{π（\sqrt{3}）^{2}}{π×4}=\frac{3}{4}$；
故答案为：$\frac{3}{4}$．
点评 本题考查了几何概型的概率求法；关键是求出区域M的面积．
练习册系列答案
相关题目
13．若双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的左、右焦点分别为F1、F2，线段F1F2被抛物线y2=2bx的焦点分成5：3两段，则此双曲线的离心率为（ ）
| A． | $\sqrt{2}$ | B． | $\frac{2\sqrt{3}}{3}$ | C． | $\frac{3\sqrt{2}}{4}$ | D． | $\sqrt{3}$ |
2017年省内事业单位面向社会公开招聘工作人员，为保证公平竞争，报名者需要参加笔试和面试两部分，且要求笔试成绩必须大于或等于90分的才有资格参加面试，90分以下（不含90分）则被淘汰．现有2000名竞聘者参加笔试，参加笔试的成绩按区间[30，50），[50，70），[70，90），[90，110），[110，130），[130，150]分段，其频率分布直方图如下图所示（频率分布直方图有污损），但是知道参加面试的人数为500，且笔试成绩在的人数为1440．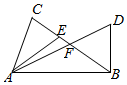
如图，F为线段BC的中点，CE=2EF，$DF=\frac{3}{5}AF$，设$\overrightarrow{AC}=a$，$\overrightarrow{AB}=b$，试用a，b表示$\overrightarrow{AE}$，$\overrightarrow{AD}$，$\overrightarrow{BD}$．