Question

4．设函数f（x）=|x-a|+|2x+2|-5（a∈R）．
（Ⅰ）试比较f（-1）与f（a）的大小；
（Ⅱ）当a=-5时，求函数f（x）的图象与轴围成的图形面积．

Answer 1

分析 （Ⅰ）f（-1）与f（a）作差化简表达式推出结果．
（Ⅱ）去掉绝对值，通过三角形的坐标，推出面积，得到结果．

解答 解：（I）因为f（a）-f（-1）=|2a+2|-5-（|a+1|-5）=|a+1|≥0，于是f（a）≥f（-1）．
当且仅当a=-1时等号成立；…5分
（Ⅱ）当a=-5时，$f（x）=|{x+5}|+|{2x+2}|-5=\left\{\begin{array}{l}3x+2，x≥-1\\-x-2，-5≤x＜-1\\-3x-12，x＜-5\end{array}\right.$，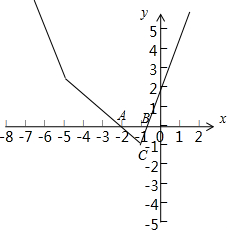
可知函数f（x）的图象和轴围成的图形是一个三角形，
其中与轴的两个交点分别为A（-2，0），$B（-\frac{2}{3}，0）$，
三角形另一顶点坐标为C（-1，-1），
从而△ABC面积为$S=\frac{1}{2}×（2-\frac{2}{3}）×1=\frac{2}{3}$．…10分
注：以上各题，其他解法请酌情给分．

点评 本题考查含绝对值代数式大小比较，绝对值函数图象特征等基础知识，以及分类讨论思想和运算求解能力，中等题．