题目内容
 关于下列命题:
关于下列命题:①若f:A→B能构成映射,则B中的任一元素在A中必须有原像;
②若实数ab>0,则函数f(x)=a•log2x+b•3x在(0,+∞)是单调函数;
③若函数y=x2的值域是{y|0≤y≤4},则它的定义域一定是{x|-2≤x≤2};
④函数f(x)=sin2xcos2x是周期为π的奇函数;
⑤如图,在平行四边形ABCD中,E、F分别是BC、CD边中点,DE与AF交于点H,设
| AB |
| a |
| AD |
| b |
| AH |
| 2 |
| 5 |
| a |
| 4 |
| 5 |
| b |
(注:把你认为正确的命题的序号都填上)
考点:命题的真假判断与应用
专题:阅读型,函数的性质及应用,平面向量及应用
分析:由映射的定义,可判断①的正确性;对a,b讨论,判断函数的单调性,即可判断②;
若函数y=x2的值域是{y|0≤y≤4},则它的定义域可以是{x|0≤x≤2},即可判断③;
运用二倍角公式,求出周期和判断奇偶性,即可判断④;
延长AF,BC相交于点G,运用相似得到AH=
AG,由向量的三角形法则即可判断⑤.
若函数y=x2的值域是{y|0≤y≤4},则它的定义域可以是{x|0≤x≤2},即可判断③;
运用二倍角公式,求出周期和判断奇偶性,即可判断④;
延长AF,BC相交于点G,运用相似得到AH=
| 2 |
| 5 |
解答:
解:①若f:A→B能构成映射,则B中的任一元素在A中不必有原像,故①错;
②若实数ab>0,a>0,b>0则函数f(x)=a•log2x+b•3x在(0,+∞)上单调递增;a<0,b<0,
函数f(x)=a•log2x+b•3x在(0,+∞)上单调递减.故②对;
③若函数y=x2的值域是{y|0≤y≤4},则它的定义域可以是{x|0≤x≤2},故③错;
④函数f(x)=sin2xcos2x=
sin4x,是周期为
的奇函数,故④错;
⑤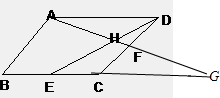 延长AF,BC相交于点G,由F为中点,CG=AD,由相似得,
延长AF,BC相交于点G,由F为中点,CG=AD,由相似得,
=
=
,AH=
AG,
=
+
=
+2
=
+2
,
则
=
+
,故⑤对.
故答案为:②⑤
②若实数ab>0,a>0,b>0则函数f(x)=a•log2x+b•3x在(0,+∞)上单调递增;a<0,b<0,
函数f(x)=a•log2x+b•3x在(0,+∞)上单调递减.故②对;
③若函数y=x2的值域是{y|0≤y≤4},则它的定义域可以是{x|0≤x≤2},故③错;
④函数f(x)=sin2xcos2x=
| 1 |
| 2 |
| π |
| 2 |
⑤
 延长AF,BC相交于点G,由F为中点,CG=AD,由相似得,
延长AF,BC相交于点G,由F为中点,CG=AD,由相似得,| AH |
| HG |
| AD |
| EG |
| 2 |
| 3 |
| 2 |
| 5 |
| AG |
| AB |
| BG |
| AB |
| AD |
| a |
| b |
则
| AH |
| 2 |
| 5 |
| a |
| 4 |
| 5 |
| b |
故答案为:②⑤
点评:本题考查函数的单调性和周期性、奇偶性和值域,考查平面向量的基本定理和映射的定义,属于较基础题.

练习册系列答案
 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案
相关题目
定义在R上的函数f(x)=
,若函数g(x)=lna-f(x)有4个不零点,则实数a的取值范围是( )
|
| A、(1,e)∪(e,+∞) | ||
B、(
| ||
C、(
| ||
D、(
|
600°的终边所在的象限为( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |