题目内容
已知函数y=
+
的定义域为M,
(Ⅰ)求M;
(Ⅱ)当x∈M时,求函数f(x)=2log22x+alog2x的最大值.
|
| 2x-2 |
(Ⅰ)求M;
(Ⅱ)当x∈M时,求函数f(x)=2log22x+alog2x的最大值.
考点:函数的最值及其几何意义
专题:转化思想,函数的性质及应用
分析:(1)根据平方根的性质,列出关于x的不等式组,求得函数的定义域,结果写成区间或集合形式;
(2)令t=log2x,则原函数化为y=2t2+at,将问题转化为二次函数在指定区间上的最值问题,因含有字母参数,注意分类讨论.
(2)令t=log2x,则原函数化为y=2t2+at,将问题转化为二次函数在指定区间上的最值问题,因含有字母参数,注意分类讨论.
解答:
解:(Ⅰ)要使函数y=
+
有意义,只需
解得:x∈[1,2].
(Ⅱ)∵f(x)=2log22x+alog2x,令t=log2x,t∈[0,1]
则函数可化为g(t)=2t2+at,t∈[0,1],其对称轴 t=-
,
当-
≤
,即a≥-2时,g(t)max=g(1)=2+a,
当-
>
,即a<-2时,g(t)max=g(0)=0,
综上可得:f(x)max=
.
|
| 2x-2 |
|
(Ⅱ)∵f(x)=2log22x+alog2x,令t=log2x,t∈[0,1]
则函数可化为g(t)=2t2+at,t∈[0,1],其对称轴 t=-
| a |
| 4 |
当-
| a |
| 4 |
| 1 |
| 2 |
当-
| a |
| 4 |
| 1 |
| 2 |
综上可得:f(x)max=
|
点评:若函数没有实际背景,则其定义域是使式子有意义的自变量的取值范围,一般是列出不等式组求解;第二问采用换元法将问题转化为二次函数的值域问题,注意分类讨论的依据是对称轴和区间的关系,一般分为区间左、区间右、区间内(若需要的话,讨论对称轴离区间左端点近、右端点近)几种情况.

练习册系列答案
相关题目
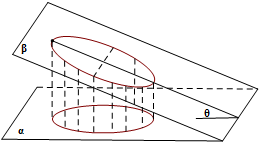 如图,一个底面半径为R的圆柱被与其底面所成角为θ(00<θ<900)的平面所截,截面是一个椭圆.当θ为30°时,这个椭圆的离心率为( )
如图,一个底面半径为R的圆柱被与其底面所成角为θ(00<θ<900)的平面所截,截面是一个椭圆.当θ为30°时,这个椭圆的离心率为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
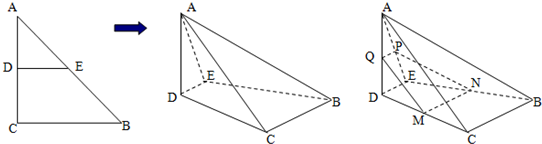
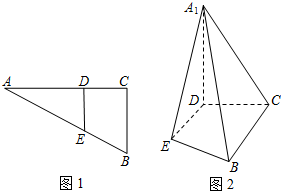 如图1直角△ABC中,两直角边长分别是BC=3,AC=6,D、E分别是AC、AB上的点,且DE∥BC,将△ADE沿DE折起到△A1DE的位置,使A1D⊥CD(如图2)
如图1直角△ABC中,两直角边长分别是BC=3,AC=6,D、E分别是AC、AB上的点,且DE∥BC,将△ADE沿DE折起到△A1DE的位置,使A1D⊥CD(如图2) 如图,四边形ABCD为平行四边形,四边形ADEF是正方形,且BD⊥平面CDE,H是BE的中点,G是AE,DF的交点.
如图,四边形ABCD为平行四边形,四边形ADEF是正方形,且BD⊥平面CDE,H是BE的中点,G是AE,DF的交点.