题目内容
对于函数f(x),若存在实数对(a,b),使得等式f(a+x)•f(a-x)=b对定义域中的每一个x都成立,则称函数f(x)是“(a,b)型函数”.
(1)判断函数f(x)=3x是否为“(a,b)型函数”,并说明理由;
(2)已知函数g(x)是“(1,4)型函数”,且当x∈[0,1]时,g(x)=x2-4x+4,当x∈[1,2],求函数h(x)=(x+2)g(x)的值域.
(1)判断函数f(x)=3x是否为“(a,b)型函数”,并说明理由;
(2)已知函数g(x)是“(1,4)型函数”,且当x∈[0,1]时,g(x)=x2-4x+4,当x∈[1,2],求函数h(x)=(x+2)g(x)的值域.
考点:抽象函数及其应用
专题:新定义,函数的性质及应用
分析:(1)根据新定义,可得到一组实数对(1,9),故存在;
(2)根据定义,得到g(1+x)•g(1-x)=4,当x∈[1,2]时,g(x)=
,其中2-x∈[0,1],由[0,1]的解析式求出g(x)在[1,2]的解析式,从而得到h(x)的解析式,配方,运用二次函数的单调性即可求出值域.
(2)根据定义,得到g(1+x)•g(1-x)=4,当x∈[1,2]时,g(x)=
| 4 |
| g(2-x) |
解答:
解:(1)函数f(x)=3x是“(a,b)型函数”.
由f(a+x)•f(a-x)=b,得3a+x•3a-x=9a=b,
故存在这样的实数对,如a=1,b=9.
(2)∵函数g(x)是“(1,4)型函数”,
∴g(1+x)•g(1-x)=4,
∴当x∈[1,2]时,g(x)=
,其中2-x∈[0,1],
而x∈[0,1]时,g(x)=x2-4x+4=(x-2)2,
∴g(2-x)=(2-x-2)2=x2,
∴g(x)=
(1≤x≤2),
∴h(x)=(x+2)•
=
+
=8(
+
)2-
,
∵1≤x≤2,∴
≤
≤1,
∴当x=1时,h(x)max=12;当x=2时,h(x)min=4,
∴当x∈[1,2],函数h(x)的值域为{4,12].
由f(a+x)•f(a-x)=b,得3a+x•3a-x=9a=b,
故存在这样的实数对,如a=1,b=9.
(2)∵函数g(x)是“(1,4)型函数”,
∴g(1+x)•g(1-x)=4,
∴当x∈[1,2]时,g(x)=
| 4 |
| g(2-x) |
而x∈[0,1]时,g(x)=x2-4x+4=(x-2)2,
∴g(2-x)=(2-x-2)2=x2,
∴g(x)=
| 4 |
| x2 |
∴h(x)=(x+2)•
| 4 |
| x2 |
| 8 |
| x2 |
| 4 |
| x |
| 1 |
| x |
| 1 |
| 4 |
| 1 |
| 2 |
∵1≤x≤2,∴
| 1 |
| 2 |
| 1 |
| x |
∴当x=1时,h(x)max=12;当x=2时,h(x)min=4,
∴当x∈[1,2],函数h(x)的值域为{4,12].
点评:本题主要考查新定义函数,正确理解定义是解题的关键,同时考查函数的解析式的求法,函数的值域的求法,是一道综合题.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
已知l是直线,α、β是两个不同平面,下列命题中的真命题是( )
| A、若l∥α,l∥β,则α∥β |
| B、若α⊥β,l∥α,则l⊥β |
| C、若l⊥α,l∥β,则α⊥β |
| D、若l∥α,α∥β,则l∥β |
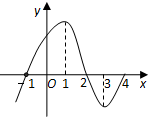 如图所示为y=f′(x)的图象,则下列判断正确的是( )
如图所示为y=f′(x)的图象,则下列判断正确的是( )①f(x)在(-∞,1)上是增函数;
②x=-1是f(x)的极小值点;
③f(x)在(2,4)上是减函数,在(-1,2)上是增函数;
④x=2是f(x)的极小值点.
| A、①②③ | B、①③④ |
| C、③④ | D、②③ |
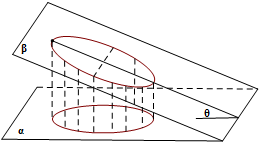 如图,一个底面半径为R的圆柱被与其底面所成角为θ(00<θ<900)的平面所截,截面是一个椭圆.当θ为30°时,这个椭圆的离心率为( )
如图,一个底面半径为R的圆柱被与其底面所成角为θ(00<θ<900)的平面所截,截面是一个椭圆.当θ为30°时,这个椭圆的离心率为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
复数z满足:z(1+i2013)=i2014(i是虚数单位),则复数z在复平面内位于( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
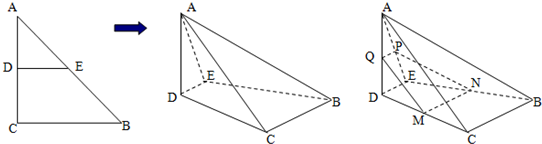
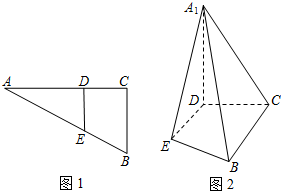 如图1直角△ABC中,两直角边长分别是BC=3,AC=6,D、E分别是AC、AB上的点,且DE∥BC,将△ADE沿DE折起到△A1DE的位置,使A1D⊥CD(如图2)
如图1直角△ABC中,两直角边长分别是BC=3,AC=6,D、E分别是AC、AB上的点,且DE∥BC,将△ADE沿DE折起到△A1DE的位置,使A1D⊥CD(如图2)