题目内容
5.在数列{an}中,an=$\frac{2{{S}_{n}}^{2}}{2{S}_{n}-1}$(n≥2),a1=1,(1)求数列{an}的通项公式;
(2)求数列{an}的前n项和Sn.
分析 (1)数列{an}中,an=$\frac{2{{S}_{n}}^{2}}{2{S}_{n}-1}$(n≥2),a1=1,(Sn-Sn-1)(2Sn-1)=2${S}_{n}^{2}$,化为:$\frac{1}{{S}_{n}}$-$\frac{1}{{S}_{n-1}}$=2,利用等差数列的通项公式可得Sn.n≥2时,an=Sn-Sn-1,可得an.
(2)由(1)可得:数列{an}的前n项和Sn.
解答 解:(1)数列{an}中,an=$\frac{2{{S}_{n}}^{2}}{2{S}_{n}-1}$(n≥2),a1=1,
∴(Sn-Sn-1)(2Sn-1)=2${S}_{n}^{2}$,化为:$\frac{1}{{S}_{n}}$-$\frac{1}{{S}_{n-1}}$=2,
∴数列{$\frac{1}{{S}_{n}}$}是等差数列,公差为2,首项为1.
∴$\frac{1}{{S}_{n}}$=1+2(n-1)=2n-1.
∴Sn=$\frac{1}{2n-1}$.
∴n≥2时,an=Sn-Sn-1=$\frac{1}{2n-1}$-$\frac{1}{2n-3}$=$\frac{-2}{(2n-1)(2n-3)}$,n=1时也成立.
∴an=$\frac{-2}{(2n-1)(2n-3)}$.
(2)由(1)可得:数列{an}的前n项和Sn=$\frac{1}{2n-1}$.
点评 本题考查了数列递推关系、等差数列的通项公式与求和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
11.已知sinα=-$\frac{12}{13}$,且α是第三象限的角,则tanα的值为( )
| A. | $\frac{12}{5}$ | B. | -$\frac{12}{5}$ | C. | $\frac{5}{12}$ | D. | -$\frac{5}{12}$ |
15.某箱子的容积V(x)与底面边长x的关系为$V(x)={x^2}•(\frac{60-x}{2})$,则当箱子的容积最大时,箱子底面边长为( )
| A. | 30 | B. | 40 | C. | 50 | D. | 以上都不正确 |
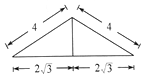
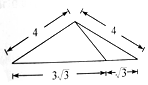
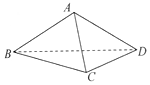 如图,在三棱锥A-BCD中,侧面ABD⊥底面BCD,BC⊥CD,AB=AD=4,BC=6,BD=4$\sqrt{3}$,该三棱锥三视图的正视图为( )
如图,在三棱锥A-BCD中,侧面ABD⊥底面BCD,BC⊥CD,AB=AD=4,BC=6,BD=4$\sqrt{3}$,该三棱锥三视图的正视图为( )

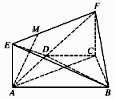 如图,在梯形ABCD中,AB∥CD,AD=CD=CB=a,∠ABC=60°,平面ACFE⊥平面ABCD,四边形ACFE是矩形,AE=a,点M在线段EF上,且MF=2EM.
如图,在梯形ABCD中,AB∥CD,AD=CD=CB=a,∠ABC=60°,平面ACFE⊥平面ABCD,四边形ACFE是矩形,AE=a,点M在线段EF上,且MF=2EM.