题目内容
6.在△ABC中,若sinA=2sinB,且a+b-$\sqrt{3}$c=0,则角C的大小为$\frac{π}{3}$.分析 根据正弦定理和余弦定理,求出cosC的值,即可得出角C的大小.
解答 解:△ABC中,若sinA=2sinB,
则a=2b;
又a+b-$\sqrt{3}$c=0,
∴3b-$\sqrt{3}$c=0,
解得c=$\sqrt{3}$b;
∴cosC=$\frac{{a}^{2}{+b}^{2}{-c}^{2}}{2ab}$
=$\frac{{4b}^{2}{+b}^{2}-{3b}^{2}}{2•2b•b}$
=$\frac{1}{2}$,
由C∈(0,π),
∴C=$\frac{π}{3}$.
故答案为:$\frac{π}{3}$.
点评 本题考查了正弦、余弦定理的应用问题,是基础题.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
14.下列说法错误的是( )
| A. | 回归直线过样本点的中心($\overline{x}$,$\overline{y}$) | |
| B. | 两个随机变量的线性相关性越强,则相关系数的绝对值就越接近于1 | |
| C. | 在回归直线方程$\stackrel{∧}{y}$=0.2x+0.8中,当解释变量x每增加1个单位时,预报变量$\stackrel{∧}{y}$平均增加0.2个单位 | |
| D. | 对分类变量X与Y,随机变量K2的观测值k越大,则判断“X与Y有关系”的把握程度越小 |
11.已知sinα=-$\frac{12}{13}$,且α是第三象限的角,则tanα的值为( )
| A. | $\frac{12}{5}$ | B. | -$\frac{12}{5}$ | C. | $\frac{5}{12}$ | D. | -$\frac{5}{12}$ |
15.平面直角坐标系中,在由x轴、$x=\frac{π}{3}$、x=$\frac{5π}{3}$和y=2所围成的矩形中任取一点,满足不等关系y≤1-sin3x的概率是( )
| A. | $\frac{4π}{3}$ | B. | $\frac{π}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
 在四棱锥S-ABCD中,底面ABCD为平行四边形,∠DBA=60°,∠SAD=30°,AD=SD=2$\sqrt{3}$,BA=BS=4.
在四棱锥S-ABCD中,底面ABCD为平行四边形,∠DBA=60°,∠SAD=30°,AD=SD=2$\sqrt{3}$,BA=BS=4.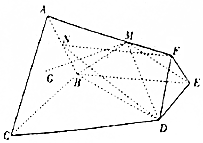 如图在棱台ABC-FED中,△DEF与△ABC分别是边长为1与2的正三角形,平面ABC⊥平面BCDE,四边形BCDE为直角梯形,BC⊥CD,CD=1,点G为△ABC的重心,N为AB的中点,点M是侧棱AF上的点且$\frac{AM}{AF}$=λ.
如图在棱台ABC-FED中,△DEF与△ABC分别是边长为1与2的正三角形,平面ABC⊥平面BCDE,四边形BCDE为直角梯形,BC⊥CD,CD=1,点G为△ABC的重心,N为AB的中点,点M是侧棱AF上的点且$\frac{AM}{AF}$=λ.