题目内容
?x∈[-1,1]使关于x的不等式x2-2m-5>0能成立,则m取值范围是 .
考点:一元二次不等式的解法
专题:不等式的解法及应用
分析:由于?x∈[-1,1]使关于x的不等式x2-2m-5>0能成立,等价转化为m<
(x2-5)max,x∈[-1,1].
| 1 |
| 2 |
解答:
解:∵?x∈[-1,1]使关于x的不等式x2-2m-5>0能成立,
∴m<
(x2-5)max,x∈[-1,1].
∴m<-2.
故答案为:(-∞,-2).
∴m<
| 1 |
| 2 |
∴m<-2.
故答案为:(-∞,-2).
点评:本题考查了恒成立问题的等价转化方法、二次函数的单调性,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
给出下列图象,其中可能为函数f(x)=x4+ax3+cx+d(a,b,c,d∈R)的图象是( )
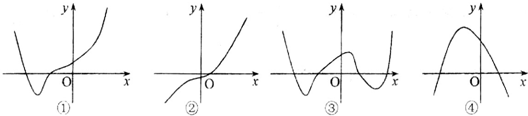

| A、①③ | B、①② | C、③④ | D、②④ |
函数f(x)=
+lg(1-x)的定义域是( )
| 1 |
| 1-x |
| A、(-1,1)∪(1,+∞) |
| B、(1,+∞) |
| C、(-∞,1) |
| D、(-∞,+∞) |
 如图,电键A、B、C、D闭合的概率分别为p1、p2、p3、p4,且彼此独立,求灯泡亮的概率.
如图,电键A、B、C、D闭合的概率分别为p1、p2、p3、p4,且彼此独立,求灯泡亮的概率.