题目内容
 已知F1,F2是椭圆
已知F1,F2是椭圆| x2 |
| a2 |
| y2 |
| b2 |
| AF1 |
| BF1 |
| 16 |
| 9 |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:椭圆的简单性质
专题:圆锥曲线的定义、性质与方程
分析:利用向量的数量积,余弦定理可解出t,再根据勾股定理即可求出∠F1AB.
解答:
解:设BF2=t,AF2=2t,
有AF1=2a-2t,BF1=2a-t,
∵
•
=(2a-t)(2a-2t)cos∠BF1A=
a2 ①
而cos∠BF1A=
=
②,
由①②得t=
a或t=-
a(舍),
∴AB=3t=a=
a,AF1=
a,BF1=
a,
可知AB2+A
=B
,
得∠F1AB=
.
故选:B
有AF1=2a-2t,BF1=2a-t,
∵
| AF1 |
| BF1 |
| 16 |
| 9 |
而cos∠BF1A=
| ||||
| 2BF1•AF1 |
| (2a-t)2+(2a-2t)2-9t2 |
| 2(2a-t)(2a-2t) |
由①②得t=
| 1 |
| 3 |
| 10 |
| 3 |
∴AB=3t=a=
| 3 |
| 3 |
| 4 |
| 3 |
| 5 |
| 3 |
可知AB2+A
| F | 2 1 |
| F | 2 1 |
得∠F1AB=
| π |
| 2 |
故选:B
点评:本题考查了向量的数量积运算以及椭圆的简单性质,属于中档题.

练习册系列答案
 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案
相关题目
已知z(1+i)=-3+4i(i为虚数单位),复数Z的共轭复数为( )
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
已知椭圆
+
=1(a>b>0)的右顶点、左焦点分别为A、F,点B(0,-b),若|
+
|=|
-
|,则椭圆的离心率值为( )
| x2 |
| a2 |
| y2 |
| b2 |
| BA |
| BF |
| BA |
| BF |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
某程序框图如图所示,当输出y值为-6时,则输出x的值为( )


| A、64 | B、32 | C、16 | D、8 |
已知f(x)是定义在R上的函数,命题p:f(x)满足?x∈R,f(-x)=-f(x),命题q:f(0)=0,则命题p是命题q的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分又不必要条件 |
已知函数f(x)=sin(ωx+
)(x∈R,ω>0)的最小正周期为4π,为了得到函数g(x)=cosωx的图象,应将f(x)的图象( )
| π |
| 6 |
A、向左平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向右平移
|
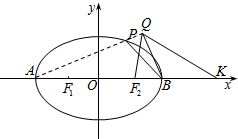 椭圆C:
椭圆C: