题目内容
13．
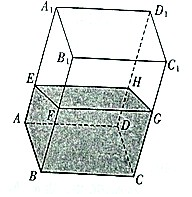如图，在透明塑料制成的长方体ABCD-A1B1C1D1容器内灌满一些水（未满），现将容器底面一边BC固定在地面上，再将容器倾斜，随着倾斜度的不同，有下列四种说法：①水的部分始终呈棱柱状
②水面四边形EFGH的面积为定值
③棱A1D1始终与水面EFGH平行
④若E∈AA1，F∈BB1，则AE+BF是定值
其中正确命题的个数是（ ）
| A． | 1个 | B． | 2个 | C． | 3 个 | D． | 4个 |
分析 ①水的部分始终呈棱柱状；从棱柱的特征平面判断即可；
②水面四边形EFGH的面积不改变；可以通过EF 的变化EH不变判断正误；
③棱A′D′始终与水面EFGH平行；利用直线与平面平行的判断定理，推出结论；
④当E∈AA′时，AE+BF是定值．通过水的体积判断即可．
解答 解：对于①，水的部分始终呈棱柱状；从棱柱的特征平面AA1B1B平行平面CC1D1D即可判断①正确；
对于②，水面四边形EFGH的面积不改变；EF是可以变化的EH不变的，所以面积是改变的，②是不正确的；
对于③，棱A1D1始终与水面EFGH平行；由直线与平面平行的判断定理，可知A1D1∥EH，所以结论正确；
对于④，当E∈AA1时，AE+BF是定值．水的体积是定值，高不变，所以底面面积不变，所以正确．
故选：C．
点评 本题是中档题，考查棱柱的结构特征，直线与平面平行的判断，棱柱的体积等知识，考查计算能力，逻辑推理能力，属于中档题．
练习册系列答案
相关题目
1．在正方体ABCD-A1B1C1D1中，AB=2，点E、F分别为AD、CD的中点，若过EF作平行于平面AB1C的平面，则所作平面在正方体表面截得的图形的周长为（ ）
| A． | $6\sqrt{2}$ | B． | $\sqrt{2}+2\sqrt{5}$ | C． | $3\sqrt{2}$ | D． | $2\sqrt{2}+2\sqrt{6}$ |
8．设定义在[-$\frac{π}{2}$，$\frac{π}{2}$]上的函数f（x）=xsinx+cosx，则不等式f（2x）＜f（x-1）的解集是（ ）
| A． | （-1，$\frac{1}{3}$） | B． | （-∞，-1）∪（$\frac{1}{3}$，+∞） | C． | [1-$\frac{π}{2}$，$\frac{1}{3}$） | D． | （-1，$\frac{π}{4}$） |
5．定积分${∫}_{0}^{1}$（ex-2x）dx的值为（ ）
| A． | e-2 | B． | e-1 | C． | e | D． | e+1 |
B．
D．