题目内容
8.设定义在[-$\frac{π}{2}$,$\frac{π}{2}$]上的函数f(x)=xsinx+cosx,则不等式f(2x)<f(x-1)的解集是( )| A. | (-1,$\frac{1}{3}$) | B. | (-∞,-1)∪($\frac{1}{3}$,+∞) | C. | [1-$\frac{π}{2}$,$\frac{1}{3}$) | D. | (-1,$\frac{π}{4}$) |
分析 求出函数的导数,得到函数的单调性,结合函数的奇偶性得到关于x的不等式,解出即可.
解答 解:f′(x)=sinx+xcosx-sinx=xcosx,
x∈[-$\frac{π}{2}$,0)时,cosx>0,f′(x)<0,
x∈(0,$\frac{π}{2}$]时,cosx≥0,f′(x)≥0,
故f(x)在[-$\frac{π}{2}$,0)递减,在(0,$\frac{π}{2}$]递增,
而f(-x)=xsinx+cosx=f(x),f(x)是偶函数,
不等式f(2x)<f(x-1),
即|2x|<|x-1|,解得:-1<x<$\frac{1}{3}$,
而$\left\{\begin{array}{l}{-\frac{π}{2}≤2x≤\frac{π}{2}}\\{-\frac{π}{2}≤x-1≤\frac{π}{2}}\end{array}\right.$,解得:1-$\frac{π}{2}$≤x≤$\frac{π}{4}$,
综上,1-$\frac{π}{2}$≤x<$\frac{1}{3}$,
故选:C.
点评 本题考查了函数的单调性、奇偶性问题,考查导数的应用,是一道中档题.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
20.在直角坐标系中,点A(1,-2),B(-2,2),则A,B两点间的距离为( )
| A. | $\sqrt{14}$ | B. | 5 | C. | $\sqrt{31}$ | D. | 25 |
16.已知全集U=Z,集合A={-3,-1,0,1,2},B={x|x=2k-1,k∈N},则A∩∁uB=( )
| A. | {0,1,2} | B. | {-3,-1,0} | C. | {-1,0,2} | D. | {-3,0,2} |
3.已知点M(2,1),直线l与圆x2+y2=4相交于P,Q两点,且|MP|=|MQ|,则直线l的斜率为( )
| A. | 2 | B. | -2 | C. | $\frac{1}{2}$ | D. | $-\frac{1}{2}$ |
17.已知sin(π+α)-3cos(2π-α)=0,则cos2α的值为( )
| A. | $\frac{4}{5}$ | B. | -$\frac{4}{5}$ | C. | $\frac{3}{5}$ | D. | -$\frac{3}{5}$ |
 的焦点到双曲线
的焦点到双曲线 的渐近线的距离不大于
的渐近线的距离不大于 ,则双曲线
,则双曲线 的离心率的取值范围是( )
的离心率的取值范围是( ) B.
B.
 D.
D.
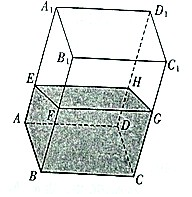 如图,在透明塑料制成的长方体ABCD-A1B1C1D1容器内灌满一些水(未满),现将容器底面一边BC固定在地面上,再将容器倾斜,随着倾斜度的不同,有下列四种说法:
如图,在透明塑料制成的长方体ABCD-A1B1C1D1容器内灌满一些水(未满),现将容器底面一边BC固定在地面上,再将容器倾斜,随着倾斜度的不同,有下列四种说法: