题目内容
18.已知扇形的圆心角为120°弧长为2cm,则这个扇形的面积等于$\frac{3}{π}$cm2.分析 利用弧长公式可求得扇形的半径,利用扇形的面积即可计算得解.
解答 解:设扇形的半径为R,
∵扇形的圆心角为$\frac{2π}{3}$,弧长为2cm,
∴$\frac{2π}{3}$R=2,解得:R=$\frac{3}{π}$,
∴扇形的面积S=$\frac{1}{2}$×2×$\frac{3}{π}$=$\frac{3}{π}$cm2.
故答案为:$\frac{3}{π}$.
点评 本题主要考查了弧长公式和扇形的面积公式的综合应用,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9.在平面直角坐标系xOy中,已知O(0,0),A($\frac{15}{4}$,0),曲线C上任一点M满足|OM|=4|AM|,点P在直线y=$\sqrt{2}$(x-1)上,如果曲线C上总存在两点到点P的距离为2,那么点P的横坐标t的范围是( )
| A. | 1<t<3 | B. | 1<t<4 | C. | 2<t<3 | D. | 2<t<4 |
7.已知函数f(x)=tan(2x+$\frac{π}{3}$),则下列说法正确的是( )
| A. | f(x)在定义域是增函数 | B. | f(x)的对称中心是($\frac{kπ}{4}$-$\frac{π}{6}$,0)(k∈Z) | ||
| C. | f(x)是奇函数 | D. | f(x)的对称轴是x=$\frac{kπ}{2}$+$\frac{π}{12}$(k∈Z) |
 ,
, ,则
,则 ( )
( ) B.
B.
 D.
D.
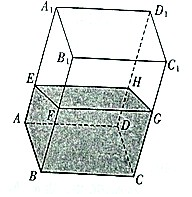 如图,在透明塑料制成的长方体ABCD-A1B1C1D1容器内灌满一些水(未满),现将容器底面一边BC固定在地面上,再将容器倾斜,随着倾斜度的不同,有下列四种说法:
如图,在透明塑料制成的长方体ABCD-A1B1C1D1容器内灌满一些水(未满),现将容器底面一边BC固定在地面上,再将容器倾斜,随着倾斜度的不同,有下列四种说法: