题目内容
6.已知向量$\overrightarrow a=({cos\frac{3x}{2},sin\frac{3x}{2}}),\overrightarrow b=({cos\frac{x}{2},sin\frac{x}{2}})$.(1)已知$\overrightarrow a$∥$\overrightarrow b$且$x∈[{0,\frac{π}{2}}]$,求x;
(2)若$f(x)=\overrightarrow a•\overrightarrow b$,写出f(x)的单调递减区间.
分析 (1)由$\overrightarrow{a}∥\overrightarrow{b}$,根据平行向量的坐标关系以及两角差的正弦公式即可得出sinx=0,这样根据x的范围便可得出x的值;
(2)进行向量数量积的坐标运算,根据两角差的余弦公式便可得出f(x)=cosx,从而可以写出余弦函数的单调递减区间.
解答 解:(1)∵$\overrightarrow{a}$∥$\overrightarrow{b}$;
∴cos$\frac{3x}{2}$sin$\frac{x}{2}$-sin$\frac{3x}{2}$cos$\frac{x}{2}$=0,即sinx=0;
∵x∈[0,$\frac{π}{2}$];
∴x=0;
(2)f(x)=$\overrightarrow{a}•\overrightarrow{b}$=cos$\frac{3x}{2}$cos$\frac{x}{2}$+sin$\frac{3x}{2}$sin$\frac{x}{2}$=cosx;
∴f(x)的单调递减区间为[2kπ,2kπ+π],k∈Z.
点评 考查平行向量的坐标关系,以及两角和与差的正余弦公式,已知三角函数值求角,向量数量积的坐标运算,以及余弦函数的单调区间.

练习册系列答案
相关题目
16.已知抛物线y2=20x的焦点到双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的一条渐近线的距离为4,则该双曲线的离心率为( )
| A. | $\frac{5}{3}$ | B. | $\frac{5}{4}$ | C. | $\sqrt{3}$ | D. | $\sqrt{5}$ |
17.下列命题中,真命题的个数是( )
①经过直线外一点有且只有一条直线与已知直线平行
②经过直线外一点有且只有一条直线与已知直线垂直
③经过平面外一点有且只有一个平面与已知平面平行
④经过平面外一点有且只有一个平面与已知平面垂直.
①经过直线外一点有且只有一条直线与已知直线平行
②经过直线外一点有且只有一条直线与已知直线垂直
③经过平面外一点有且只有一个平面与已知平面平行
④经过平面外一点有且只有一个平面与已知平面垂直.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
14.若正实数m、n满足3m+4n=5mn,则m+3n的最小值是( )
| A. | 4 | B. | 5 | C. | $\frac{24}{5}$ | D. | $\frac{28}{5}$ |
1. 执行如图的程序框图,若输入k=63,则输出的n=( )
执行如图的程序框图,若输入k=63,则输出的n=( )
 执行如图的程序框图,若输入k=63,则输出的n=( )
执行如图的程序框图,若输入k=63,则输出的n=( )| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
11.设全集U={x∈N|x≥1},集合A={x∈N|x2≥3},则∁UA=( )
| A. | ∅ | B. | {1} | C. | {1,2} | D. | {1,2,3} |
18.复数z满足(z-1)(1+i)=2i,则|z|=( )
| A. | 1 | B. | 2 | C. | $\sqrt{5}$ | D. | 5 |
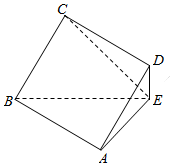 如图,四边形ABCD是正方形,DE⊥平面ABE,BE=3DE,DE=3,AB⊥AE.
如图,四边形ABCD是正方形,DE⊥平面ABE,BE=3DE,DE=3,AB⊥AE.