题目内容
16.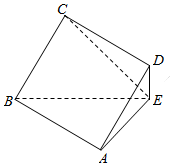 如图,四边形ABCD是正方形,DE⊥平面ABE,BE=3DE,DE=3,AB⊥AE.
如图,四边形ABCD是正方形,DE⊥平面ABE,BE=3DE,DE=3,AB⊥AE.(I)求证:AB⊥面ADE;
(Ⅱ)求二面角A-BC-E的平面角的正弦值.
分析 (1)根据线面垂直的判定定理即可证明AB⊥面ADE;
(2)建立空间坐标系,利用向量法求出平面的法向量,利用向量法进行求解即可.
解答  证明:(I)∵DE⊥平面ABE,AB?平面ABE,
证明:(I)∵DE⊥平面ABE,AB?平面ABE,
∴DE⊥AB,
∵AB⊥AE,DE∩AE=E,
∴AB⊥面ADE
(Ⅱ)∵BE=3DE,DE=3,AB⊥AE.
∴BE=9,设正方形ABCD的边长为x,
则AE2=AD2-DE2=BE2-AB2,
即x2-9=81-x2,
即2x2=90,x2=45,
则x=3$\sqrt{5}$,则AE=6,AB=3$\sqrt{5}$
建立以E为坐标原点,EA,ED分别为x,z轴的空间直角坐标系如图:
则E(0,0,0),A(6,0,0),B(6,-3$\sqrt{5}$,0),D(0,0,3),
设C(x,y,z),
则$\overrightarrow{DC}$=$\overrightarrow{AB}$,
即(x,y,z-3)=(0,-3$\sqrt{5}$,0),
即x=0,y=-3$\sqrt{5}$,z=3,
即C(0,-3$\sqrt{5}$,3),
设平面ABC的法向量为$\overrightarrow{m}$=(x,y,z),
则$\overrightarrow{AB}$=(0,-3$\sqrt{5}$,0),$\overrightarrow{BC}$=$\overrightarrow{AD}$=(-6,0,3)
则由$\overrightarrow{m}$•$\overrightarrow{AB}$=0,$\overrightarrow{m}$•$\overrightarrow{BC}$=0,得$\left\{\begin{array}{l}{-3\sqrt{5}y=0}\\{-6x+3z=0}\end{array}\right.$,即$\left\{\begin{array}{l}{y=0}\\{z=2x}\end{array}\right.$
令x=1,则y=0,z=2,则$\overrightarrow{m}$=(1,0,2),
同理设平面BCE的法向量为$\overrightarrow{n}$=(x,y,z),
$\overrightarrow{BC}$=$\overrightarrow{AD}$=(-6,0,3),$\overrightarrow{EB}$=(6,-3$\sqrt{5}$,0),
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{BC}=0}\\{\overrightarrow{n}•\overrightarrow{EB}=0}\end{array}\right.$,得$\left\{\begin{array}{l}{-6x+3z=0}\\{6x-3\sqrt{5}y=0}\end{array}\right.$,即$\left\{\begin{array}{l}{z=2x}\\{y=\frac{2\sqrt{5}}{5}x}\end{array}\right.$,
令x=5,则y=2$\sqrt{5}$,z=10,则$\overrightarrow{n}$=(5,2$\sqrt{5}$,10),
则cos<$\overrightarrow{m}$,$\overrightarrow{n}$>=$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}|•|\overrightarrow{n}|}$=$\frac{5+2×10}{\sqrt{1+{2}^{2}}•\sqrt{{5}^{2}+(2\sqrt{5})^{2}+1{0}^{2}}}$=$\frac{25}{\sqrt{5}•\sqrt{5×29}}$=$\frac{5}{\sqrt{29}}$=$\frac{5\sqrt{29}}{29}$,
则二面角A-BC-E的平面角的正弦值sin<$\overrightarrow{m}$,$\overrightarrow{n}$>=$\sqrt{1-(\frac{5}{\sqrt{29}})^{2}}$=$\sqrt{\frac{4}{29}}$=$\frac{2\sqrt{29}}{29}$.
点评 本题主要考查直线垂直的判定以及二面角的求解,建立空间直角坐标系,利用向量法进行求解,综合性较强,运算量较大.

| A. | $(-∞,\frac{1}{2})∪(2,+∞)$ | B. | $(-∞,\frac{1}{2}]∪[2,+∞)$ | C. | $[\frac{1}{2},2]$ | D. | $(\frac{1}{2},2)$ |
| 零件数x(个) | 10 | 20 | 30 | 40 | 50 |
| 加工时间y(分钟) | 62 | 68 | 75 | 81 | 89 |
(Ⅱ)根据(I)所求回归直线方程,预测此车间加工这种件70个时,所需要的加工时间.
附:b=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-{n\overline{x}}^{2}}$,$\overline{y}$=b$\overline{x}$+a.
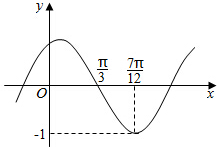 函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的图象如图所示.
函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的图象如图所示.