题目内容
已知向量
=(2sin(ωx+
),2),
=(2cosωx,0)(ω>0),函数f(x)=
•
的图象与直线y=-2+
的相邻两个交点之间的距离为π.
(1)求ω的值;
(2)求函数f(x)在[0,π]上的单调递增区间.
| a |
| 2π |
| 3 |
| b |
| a |
| b |
| 3 |
(1)求ω的值;
(2)求函数f(x)在[0,π]上的单调递增区间.
考点:平面向量数量积的运算,三角函数中的恒等变换应用
专题:三角函数的图像与性质,平面向量及应用
分析:(1)利用数量积运算性质、倍角公式、两角和差的正弦公式、三角函数的图象与性质即可得出;
(2)利用余弦函数的单调性即可得出.
(2)利用余弦函数的单调性即可得出.
解答:
解:(1)函数f(x)=
•
=4sin(ωx+
)cosωx
=4(-
sinωx+
cosωx)cosωx
=-sin2ωx+2
cos2ωx
=-sin2ωx+
(1+cos2ωx)
=2cos(2ωx+
)+
,
∵函数f(x)=
•
的图象与直线y=-2+
的相邻两个交点之间的距离为π.
∴T=π,
∴
=π,解得ω=1.
因此ω=1.
(2)由(1)可得f(x)=2cos(2x+
)+
,
由x∈[0,π]得(2x+
)∈[
,
],
故(2x+
)∈[π,2π]时,f(x)单调递增,
即f(x)的单调增区间为[
,
].
| a |
| b |
| 2π |
| 3 |
=4(-
| 1 |
| 2 |
| ||
| 2 |
=-sin2ωx+2
| 3 |
=-sin2ωx+
| 3 |
=2cos(2ωx+
| π |
| 6 |
| 3 |
∵函数f(x)=
| a |
| b |
| 3 |
∴T=π,
∴
| 2π |
| 2ω |
因此ω=1.
(2)由(1)可得f(x)=2cos(2x+
| π |
| 6 |
| 3 |
由x∈[0,π]得(2x+
| π |
| 6 |
| π |
| 6 |
| 13π |
| 6 |
故(2x+
| π |
| 6 |
即f(x)的单调增区间为[
| 5π |
| 12 |
| 11π |
| 12 |
点评:本题考查了数量积运算性质、倍角公式、两角和差的正弦公式、三角函数的图象与性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
已知f(x)是定义在R上的奇函数,当0≤x≤1时,f(x)=x2,当x>0时,f(x+1)=f(x)+1,若直线y=kx与函数y=f(x)的图象恰有9个不同的公共点,则实数k的值为( )
A、2
| ||
B、2
| ||
C、2
| ||
D、2
|
已知向量
=(1,2),
=(2x,-3),若
⊥(
+
),则x=( )
| a |
| b |
| a |
| a |
| b |
| A、3 | ||
B、-
| ||
| C、-3 | ||
D、
|
已知向量
,
满足|
-
|=
,
•
=1,则|
+
|=( )
| a |
| b |
| a |
| b |
| 6 |
| a |
| b |
| a |
| b |
A、
| ||
B、2
| ||
C、
| ||
| D、10 |
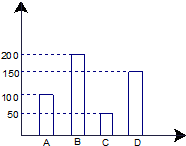 某工厂2014年第一季度生产的A、B、C、D四种型号的产品产量用条形图表示如图,现用分层抽样的方法从中选取50件样品参加四月份的一个展销会.
某工厂2014年第一季度生产的A、B、C、D四种型号的产品产量用条形图表示如图,现用分层抽样的方法从中选取50件样品参加四月份的一个展销会.