题目内容
已知f(x)是定义在R上的奇函数,当0≤x≤1时,f(x)=x2,当x>0时,f(x+1)=f(x)+1,若直线y=kx与函数y=f(x)的图象恰有9个不同的公共点,则实数k的值为( )
A、2
| ||
B、2
| ||
C、2
| ||
D、2
|
考点:抽象函数及其应用,函数的零点与方程根的关系
专题:函数的性质及应用
分析:本题通过奇函数特征得到函数图象经过原点,且关于原点对称,利用f(x+1)=f(x)+f(1)得到函数类似周期性特征,从而可以画出函数的草图,得到k的取值
解答:
 解:∵当0≤x≤1时,f(x)=x2,
解:∵当0≤x≤1时,f(x)=x2,
∴f(1)=1.
∵当x>0时,f(x+1)=f(x)+f(1),
∴f(x+1)=f(x)+1,
∴当x∈[n,n+1],n∈N*时,
f(x+1)=f(x-1)+1=f(x-2)+2=…=f(x-n)+n=(x-n)2+n,
∵函数f(x)是定义在R上的奇函数,
∴函数图象经过原点,且关于原点对称.
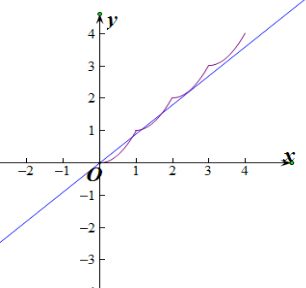
∵直线y=kx与函数y=f(x)的图象恰有9个不同的公共点,
∴当x>0时,直线y=kx与函数y=f(x)的图象恰有4个不同的公共点,
∴由x>0时f(x)的图象可知:
直线y=kx与函数y=f(x)的图象相切位置在x∈[2,3]时,直线y=kx与函数y=f(x)的图象恰有9个不同的公共点,
由
得:
x2-(k+4)x+6=0,
令△=0,得:k=2
-4.
故选:C
 解:∵当0≤x≤1时,f(x)=x2,
解:∵当0≤x≤1时,f(x)=x2,∴f(1)=1.
∵当x>0时,f(x+1)=f(x)+f(1),
∴f(x+1)=f(x)+1,
∴当x∈[n,n+1],n∈N*时,
f(x+1)=f(x-1)+1=f(x-2)+2=…=f(x-n)+n=(x-n)2+n,
∵函数f(x)是定义在R上的奇函数,
∴函数图象经过原点,且关于原点对称.
∵直线y=kx与函数y=f(x)的图象恰有9个不同的公共点,
∴当x>0时,直线y=kx与函数y=f(x)的图象恰有4个不同的公共点,
∴由x>0时f(x)的图象可知:
直线y=kx与函数y=f(x)的图象相切位置在x∈[2,3]时,直线y=kx与函数y=f(x)的图象恰有9个不同的公共点,
由
|
x2-(k+4)x+6=0,
令△=0,得:k=2
| 6 |
故选:C
点评:本题考查抽象函数及其应用,着重考查函数的零点与方程根的关系,考查函数的对称性、周期性、奇偶性的综合应用,考查转化思想与作图能力,属于难题.

练习册系列答案
相关题目
已知O为△ABC外一点,D为BC边上一点,且
+
-2
=0,若AB=3,AC=5.则
•
=( )
| OC |
| OB |
| OD |
| AD |
| BC |
| A、-8 | B、8 | C、-2 | D、2 |
设A(1,2),B(3,-1),C(3,4),则
•
( )
| AB |
| AC |
| A、11 | B、5 | C、-2 | D、1 |
已知函数f(x)=3-2|x|,g(x)=x2,构造函数F(x)=
,那么函数y=F(x)( )
|
| A、有最大值1,最小值-1 |
| B、有最小值-1,无最大值 |
| C、有最大值1,无最小值 |
| D、有最大值3,最小值1 |
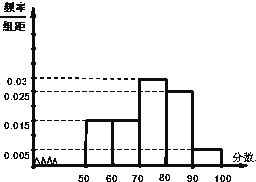 高二年级从参加期末考试的学生中抽出60名学生,并统计了他们的物理成绩(成绩均为整数且满分为100分),把其中不低于50分的分成五段[50,60),[60,70)…[90,100]后画出如下部分频率分布直方图.观察图形的信息,回答下列问题:
高二年级从参加期末考试的学生中抽出60名学生,并统计了他们的物理成绩(成绩均为整数且满分为100分),把其中不低于50分的分成五段[50,60),[60,70)…[90,100]后画出如下部分频率分布直方图.观察图形的信息,回答下列问题: