题目内容
12．在等比数列{an}中，a1+a3=5，a2+a4=10，则数列{an}的前6项的和为63．分析 利用等比数列的通项公式即可得出首项和公比；利用等比数列的求和公式即可得出结果．
解答 解：设等比数列{an}的公比为q，
∵a1+a3=5，a2+a4=10，
∴q（a1+a3）=5q=10，
解得q=2，a1=1．
则该数列的前6项的和S6=$\frac{1-{2}^{6}}{1-2}$=63．
故答案为：63．
点评 本题考查了等比数列的通项公式及其求和公式，考查了推理能力与计算能力，属于基础题．
练习册系列答案
亮点激活精编提优100分大试卷系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
2．若$\overrightarrow a=（1，2）$，$\overrightarrow b=（m，1）$，若$\overrightarrow a⊥\overrightarrow b$，则m=（ ）
| A． | $-\frac{1}{2}$ | B． | $\frac{1}{2}$ | C． | 2 | D． | -2 |
3．数列{an}的通项公式为an=3n-23，当Sn取到最小时，n=（ ）
| A． | 5 | B． | 6 | C． | 7 | D． | 8 |
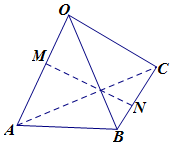如图，已知三棱锥O-ABC，OA=4，OB=5，OC=3，∠AOB=∠BOC=60°，∠COA=90°，M，N分别是OA，BC的中点，设$\overrightarrow{OA}$=a，$\overrightarrow{OB}$=b，$\overrightarrow{OC}$=c．
1．对于在R上可导的任意函数f（x），若其导函数为f′（x），且满足（x-1）f′（x）≥0，则必有（ ）
| A． | f（0）+f（2）≤2f（1） | B． | f（0）+f（2）＜2f（1） | C． | f（0）+f（2）≥2f（1） | D． | f（0）+f（2）＞2f（1） |