题目内容
3.数列{an}的通项公式为an=3n-23,当Sn取到最小时,n=( )| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
分析 令an=3n-23≤0,解出即可得出.
解答 解:令an=3n-23≤0,解得n$≤\frac{23}{3}$=7+$\frac{2}{3}$.
∴当Sn取到最小时,n=7.
故选:C.
点评 本题考查了数列的通项公式与求和公式、数列的单调性,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
14.设α是第二象限角,cosα=-$\frac{3}{5}$,则tanα=( )
| A. | $\frac{4}{3}$ | B. | $\frac{3}{4}$ | C. | -$\frac{3}{4}$ | D. | -$\frac{4}{3}$ |
15.已知函数f(x)=ax-1+4的图象恒过定点P,则点P的坐标是( )
| A. | (1,5) | B. | (1,4) | C. | (0,4) | D. | (4,0) |
13.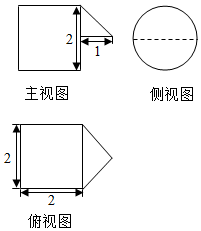 某几何体的三视图如图所示,则该几何体的体积为( )
某几何体的三视图如图所示,则该几何体的体积为( )
 某几何体的三视图如图所示,则该几何体的体积为( )
某几何体的三视图如图所示,则该几何体的体积为( )| A. | $\frac{1}{3}+2π$ | B. | $\frac{13}{6}π$ | C. | $\frac{7π}{3}$ | D. | $\frac{5π}{2}$ |
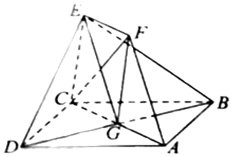 (理)如图,正方形ABCD和四边形ACEF所在的平面互相垂直,CE⊥AC,EF∥AC,EF=CE,AB=$\sqrt{2}$EF.
(理)如图,正方形ABCD和四边形ACEF所在的平面互相垂直,CE⊥AC,EF∥AC,EF=CE,AB=$\sqrt{2}$EF.