题目内容
1．对于在R上可导的任意函数f（x），若其导函数为f′（x），且满足（x-1）f′（x）≥0，则必有（ ）| A． | f（0）+f（2）≤2f（1） | B． | f（0）+f（2）＜2f（1） | C． | f（0）+f（2）≥2f（1） | D． | f（0）+f（2）＞2f（1） |
分析 函数f（x）满足（x-1）f′（x）≥0，对x与1的大小关系分类讨论即可得出函数f（x）的单调性．
解答 解：∵函数f（x）满足（x-1）f′（x）≥0，
∴x＞1时，f′（x）≥0，此时函数f（x）单调递增；
x＜1时，f′（x）≤0，此时函数f（x）单调递减，
因此x=1函数f（x）取得极小值．
∴f（0）≥f（1），f（2）≥f（1），
∴f（0）+f（2）≥2 f（1），
故选：C．
点评 本题考查了利用导数研究函数的单调性，考查了分类讨论方法、推理能力与计算能力，属于中档题．
练习册系列答案
教材全解字词句篇系列答案
相关题目
16．|$\overrightarrow{a}$|=2，向量$\overrightarrow{a}$与向量$\overrightarrow{b}$的夹角为120°，则向量$\overrightarrow{a}$在向量$\overrightarrow{b}$方向上的投影等于（ ）
| A． | 2 | B． | 1 | ||
| C． | -1 | D． | 由向量 b 的长度确定 |
6．在（x-1）n（n∈N+）的二项展开式中，若只有第4项的二项式系数最大，则${（{2\sqrt{x}-\frac{1}{{\sqrt{x}}}}）^n}$的二项展开式中的常数项为（ ）
| A． | 960 | B． | -160 | C． | -560 | D． | -960 |
13．
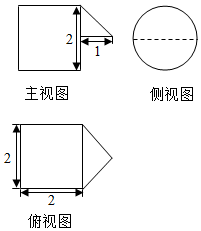某几何体的三视图如图所示，则该几何体的体积为（ ）
某几何体的三视图如图所示，则该几何体的体积为（ ）| A． | $\frac{1}{3}+2π$ | B． | $\frac{13}{6}π$ | C． | $\frac{7π}{3}$ | D． | $\frac{5π}{2}$ |