题目内容
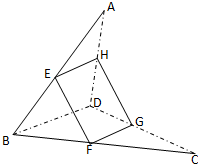 如图,已知四边形ABCD是空间四边形,E是AB的中点,F,G分别是BC,CD上的点,且
如图,已知四边形ABCD是空间四边形,E是AB的中点,F,G分别是BC,CD上的点,且| CF |
| CB |
| CG |
| CD |
| 1 |
| 3 |
(1)若AD=λAH. 求λ的值;
(2)试判断四边形EFGH的形状;并给出证明.
考点:直线与平面平行的性质
专题:空间位置关系与距离
分析:(1)由已知条件推导出FG∥BD,且FG=
BD,再利用直线与平面平行的性质定理和平行公理能求出λ.
(2)四边形EFGH为梯形,利用平行公理和梯形定义进行说明.
| 1 |
| 3 |
(2)四边形EFGH为梯形,利用平行公理和梯形定义进行说明.
解答:
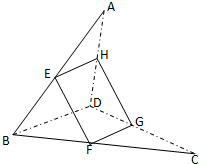 解:(1)∵
解:(1)∵
=
=
,
∴FG∥BD,且FG=
BD,
∵FG不包含于平面ABD,BD?平面ABD,
∴由直线与平面平行的性质定理,知:FG∥EH,
由平行公理知:EH∥BD,
∵E是AB的中点,∴H是AD的中点,
∴AD=2AH,∴λ=2.
(2)四边形EFGH为梯形,理由如下:
由(1)知FG∥BD,EH∥BD,
∴EH∥FG,
又∵FG=
BD,EH=
BD,
∴EH=
FG,
∴四边形EFGH为梯形.
 解:(1)∵
解:(1)∵| CF |
| CB |
| CG |
| CD |
| 1 |
| 3 |
∴FG∥BD,且FG=
| 1 |
| 3 |
∵FG不包含于平面ABD,BD?平面ABD,
∴由直线与平面平行的性质定理,知:FG∥EH,
由平行公理知:EH∥BD,
∵E是AB的中点,∴H是AD的中点,
∴AD=2AH,∴λ=2.
(2)四边形EFGH为梯形,理由如下:
由(1)知FG∥BD,EH∥BD,
∴EH∥FG,
又∵FG=
| 1 |
| 3 |
| 1 |
| 2 |
∴EH=
| 3 |
| 2 |
∴四边形EFGH为梯形.
点评:本题考查参数值的求法,考查四边形形状的判断,解题时要认真审题,注意平行公理的合理运用.

练习册系列答案
相关题目
已知f(x)是定义在(-∞,+∞)上的函数,导函数f′(x)满足f′(x)<f(x)对于x∈R恒成立,则( )
| A、f(2)>e2f(0),f(2011)>e2011f(0) |
| B、f(2)<e2f(0),f(2011)>e2011f(0) |
| C、f(2)>e2f(0),f(2011)<e2011f(0) |
| D、f(2)<e2f(0),f(2011)<e2011f(0) |
 四棱锥S-ABCD中,底面ABCD为平行四边形,侧面SBC⊥底面ABCD.E为SD的中点,已知∠ABC=45°,AB=2,
四棱锥S-ABCD中,底面ABCD为平行四边形,侧面SBC⊥底面ABCD.E为SD的中点,已知∠ABC=45°,AB=2,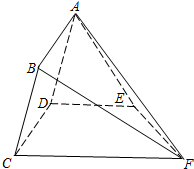 如图,矩形ABCD所在的半平面和直角梯形CDEF所在的半平面成60°的二面角,DE∥CF,CD⊥DE,AD=2,
如图,矩形ABCD所在的半平面和直角梯形CDEF所在的半平面成60°的二面角,DE∥CF,CD⊥DE,AD=2,