题目内容
已知直线l1:2x+ay=2,l2:a2x+2y=1且l1⊥l2,则a= .
考点:直线的一般式方程与直线的垂直关系
专题:直线与圆
分析:当a=0时,直接验证是否满足垂直的条件;当a≠0时,利用直线垂直于斜率之间的关系即可得出.
解答:
解:当a=0时,直线l1:x=1,l2:2y=1,此时满足l1⊥l2,因此a=0适合题意;
当a≠0时,直线l1:2x+ay=2,化为y=-
x+
,可得斜率k1=-
,
l2:a2x+2y=1化为y=-
x+
,可得斜率k2=-
.
∵l1⊥l2,∴k1k2=-
•(-
)=a=-1,解得a=-1.
综上可得:a=0或-1.
当a≠0时,直线l1:2x+ay=2,化为y=-
| 2 |
| a |
| 2 |
| a |
| 2 |
| a |
l2:a2x+2y=1化为y=-
| a2 |
| 2 |
| 1 |
| 2 |
| a2 |
| 2 |
∵l1⊥l2,∴k1k2=-
| 2 |
| a |
| a2 |
| 2 |
综上可得:a=0或-1.
点评:本题考查了直线垂直于斜率之间的关系和分类讨论的思想方法,考查了推理能力和计算能力,属于基础题.

练习册系列答案
相关题目
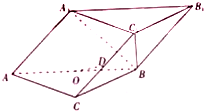 三棱柱ABC-A1B1C1中,平面A1ABB1⊥平面ABC,O是AB的中点.
三棱柱ABC-A1B1C1中,平面A1ABB1⊥平面ABC,O是AB的中点.