题目内容
平面α与β交于直线MN，P为两平面外一点，过P分别作平面α，β的垂线PA、PB，A、B为垂足，若PA=6，PB=4，∠APB=60°，求P到直线MN的距离．
考点：点、线、面间的距离计算
专题：计算题,空间位置关系与距离
分析：设平面PAB与MN交于O，则MN⊥平面PAB，MN⊥PO，PO即为所求，且为PAOB外接圆的直径，利用余弦定理求出AB，再用正弦定理求OP．
解答：
解：由题意，设平面PAB与MN交于O，则MN⊥平面PAB，
∴MN⊥PO，PO即为所求，且为PAOB外接圆的直径．
△PAB中，PA=6，PB=4，∠APB=60°，∴AB=
=2
，
∴由正弦定理可得OP=
=
．
∴MN⊥PO，PO即为所求，且为PAOB外接圆的直径．
△PAB中，PA=6，PB=4，∠APB=60°，∴AB=
36+16-2•6•4•
|
| 7 |
∴由正弦定理可得OP=
2
| ||||
|
4
| ||
| 3 |
点评：本题考查点、线、面间的距离计算，考查正弦定理、余弦定理，考查学生分析解决问题的能力，比较基础．
练习册系列答案
相关题目
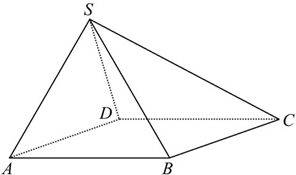（能力挑战题）如图，已知四棱锥S-ABCD的底面ABCD是菱形，∠BAD=60°，且SA=SB=SD=AB=2．