题目内容
13.若数列{an}的前n项和为${S_n}=\frac{{n{a_n}}}{2},{a_2}=2$,则数列{an}的通项公式是an=2(n-1).分析 求得a1=0,当n≥3时,an=Sn-Sn-1=$\frac{n{a}_{n}}{2}$-$\frac{(n-1){a}_{n-1}}{2}$,整理得:$\frac{{a}_{n}}{{a}_{n-1}}$=$\frac{n-1}{n-2}$,采用累乘法,即可求得an=2(n-1),当n=1和n=2时,显然成立,即可求得数列{an}的通项公式.
解答 解:由当n=2时,a1+a2=$\frac{2×{a}_{2}}{2}$,则a1=0,
当n≥3时,由Sn-1=$\frac{(n-1){a}_{n-1}}{2}$,则an=Sn-Sn-1=$\frac{n{a}_{n}}{2}$-$\frac{(n-1){a}_{n-1}}{2}$,
整理得:$\frac{{a}_{n}}{{a}_{n-1}}$=$\frac{n-1}{n-2}$,
则$\frac{{a}_{3}}{{a}_{2}}$=$\frac{2}{1}$,
$\frac{{a}_{4}}{{a}_{3}}$=$\frac{3}{2}$,
…
$\frac{{a}_{n}}{{a}_{n-1}}$=$\frac{n-1}{n-2}$,
以上各式相乘可得:$\frac{{a}_{3}}{{a}_{2}}$×$\frac{{a}_{4}}{{a}_{3}}$×…×$\frac{{a}_{n}}{{a}_{n-1}}$=$\frac{2}{1}$×$\frac{3}{2}$×…×$\frac{n-1}{n-2}$,
∴$\frac{{a}_{n}}{{a}_{2}}$=n-1,则an=2(n-1),
当n=1和n=2时,显然成立,
数列{an}的通项公式an=2(n-1),
故答案为:an=2(n-1).
点评 本题考查数列的通项公式的求求法,考查累乘法求数列的通项公式,考查计算能力,属于中档题.

| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | -$\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
| A. | 8 | B. | 7 | C. | 6 | D. | 5 |
| A. | 一解 | B. | 二解 | C. | 无解 | D. | 一解或二解 |
| A. | i | B. | -i | C. | 1 | D. | -1 |
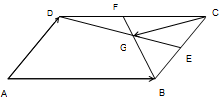 如图,在平行四边形ABCD中,E、F分别为BC与DC中点,G为BF与DE交点,若$\overrightarrow{AB}=\overrightarrow a$,$\overrightarrow{AD}=\overrightarrow b$,试以$\overrightarrow a$,$\overrightarrow b$为基底表示下面向量
如图,在平行四边形ABCD中,E、F分别为BC与DC中点,G为BF与DE交点,若$\overrightarrow{AB}=\overrightarrow a$,$\overrightarrow{AD}=\overrightarrow b$,试以$\overrightarrow a$,$\overrightarrow b$为基底表示下面向量