题目内容
计算2-(
)+
+
-
;
用列举法表示集合{x∈Z|
∈Z}.
| 1 |
| 2 |
| (-4)0 | ||
|
| 1 | ||
|
(1-
|
用列举法表示集合{x∈Z|
| 6 |
| 6-x |
考点:有理数指数幂的运算性质,集合的表示法
专题:集合
分析:(1)利用指数幂的运算法则即可得出;
(2)由于6-x是6的质因数,可得6-x=±1,±2,±3,±6,即可得出.
(2)由于6-x是6的质因数,可得6-x=±1,±2,±3,±6,即可得出.
解答:
解:(1)原式=
+
+
+1-1=2
.
(2)6-x是6的质因数,∴6-x=±1,±2,±3,±6.
∴列举法表示集合{x∈Z|
∈Z}={-6,-3,-2,-1,1,2,3,6}.
| 1 | ||
|
| 1 | ||
|
| 2 |
| 2 |
(2)6-x是6的质因数,∴6-x=±1,±2,±3,±6.
∴列举法表示集合{x∈Z|
| 6 |
| 6-x |
点评:本题考查了指数幂的运算法则、质因数,属于基础题.

练习册系列答案
相关题目
已知sin(
-x)=
,则cos(x+
)=( )
| π |
| 3 |
| 3 |
| 5 |
| π |
| 6 |
A、-
| ||
B、-
| ||
C、
| ||
D、
|
下列函数中为偶函数,且在区间(0,+∞)上为增函数的是( )
| A、y=3-x | ||
| B、y=|x| | ||
C、
| ||
| D、y=-x2+4 |
设等差数列{an}满足:a1+a4+a7=12,则a1+a2+a3+…+a7=( )
| A、14 | B、21 | C、28 | D、35 |
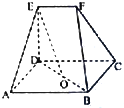 已知矩形ABCD,ED⊥平面ABCD,EF∥DC,EF=DE=AD=
已知矩形ABCD,ED⊥平面ABCD,EF∥DC,EF=DE=AD=