题目内容
已知集合A={x|a-1≤x≤a+2}，B={x|3＜x＜5}，若A∩B=B，求实数a的取值范围．
考点：交集及其运算
专题：集合
分析：由A∩B=B，得B⊆A，然后利用集合端点值间的关系列不等式组得答案．
解答：
解：∵A={x|a-1≤x≤a+2}，B={x|3＜x＜5}，
由A∩B=B，得B⊆A，
∴
，解得3≤a≤4．
∴实数a的取值范围是[3，4]．
由A∩B=B，得B⊆A，
∴
|
∴实数a的取值范围是[3，4]．
点评：本题考查了交集及其运算，关键是由集合间的关系列出正确的不等式组，是基础题．
练习册系列答案
相关题目
“a2＞b3是“a4＞b6”的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
过点（π，1）且与曲线y=sinx+cosx在点（
，1）处的切线垂直的直线方程为（ ）
| π |
| 2 |
| A、y=x-1+π |
| B、y=x+1-π |
| C、y=-x+1+π |
| D、y=-x-1+π |
曲线y=x3在点P处的切线斜率为k=3，则点P的坐标为（ ）
| A、（2，8） |
| B、（-2，-8） |
| C、p（X=2）=P |
| D、（1，1）或（-1，-1） |
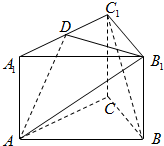如图，正三棱柱ABC-A1B1C1的底面边长为a，侧棱长为