题目内容
3．
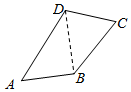如图，已知四边形ABCD中，AB=CD=1，AD=$\sqrt{2}$BC=2，∠A+∠C=$\frac{3π}{4}$．则BD的长为$\frac{\sqrt{65}}{5}$．
分析 利用两次余弦公式，求得3cosA+sinA=1，将∠C=$\frac{3π}{4}$∠A，代入求得cosA=$\frac{3}{5}$的值，可求得BD．
解答 解：在△ABD中由余弦定理可知：BD2=AB2+AD2-2AB•AD•cosA，
在△CDB中与余弦定理可知：BD2=DC2+BC2-2AB•AD•cosC，
将AB=CD=1，AD=$\sqrt{2}$BC=2代入，整理得：2cosA-$\sqrt{2}$cosC=1，∠A+∠C=$\frac{3π}{4}$，
2cosA-$\sqrt{2}$cos（$\frac{3π}{4}$-A）=1，
整理得：3cosA+sinA=1，
两边平方（3cosA+sinA）2=9cos2A+6cosAsinA+sin2A=cos2A+sin2A，
整理得：sinA=-$\frac{4}{3}cosA$，
cosA=$\frac{3}{5}$，
BD=$\sqrt{4+1-4×\frac{3}{5}}$，
BD=$\frac{\sqrt{65}}{5}$，
故答案为：$\frac{\sqrt{65}}{5}$．
点评 本题考查余弦定理及三角恒等变换，属于中档题．
练习册系列答案
相关题目
14．已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1的渐近线方程为y=$±\frac{1}{3}x$，则此双曲线的离心率为（ ）
| A． | $\frac{{2\sqrt{2}}}{3}$ | B． | $\frac{{\sqrt{10}}}{3}$ | C． | 3 | D． | $\sqrt{10}$ |
11．已知圆C的圆心与双曲线4x2-$\frac{4}{3}{y^2}$=1的左焦点重合，又直线4x-3y-6=0与圆C相切，则圆C的标准方程为（ ）
| A． | （x-1）2+y2=4 | B． | （x+1）2+y2=2 | C． | （x+1）2+y2=1 | D． | （x+1）2+y2=4 |
18．数列{an}满足a1=1，且an+1=a1+an+n（n∈N*），则$\frac{1}{{a}_{1}}$+$\frac{1}{{a}_{2}}$+…+$\frac{1}{{a}_{2016}}$等于（ ）
| A． | $\frac{2015}{2016}$ | B． | $\frac{4028}{2015}$ | C． | $\frac{4032}{2017}$ | D． | $\frac{2014}{2015}$ |
8．已知双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的一条渐近线的斜率为-2，则C的离心率e=（ ）
| A． | $\frac{2\sqrt{3}}{3}$ | B． | $\frac{\sqrt{5}}{2}$ | C． | 2 | D． | $\sqrt{5}$ |
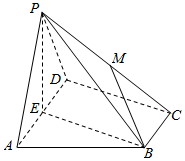如图，在四棱锥P-ABCD中，底面ABCD为直角梯形，AD∥BC，∠ADC=90°，平面PAD⊥底面ABCD，E为AD的中点，M是棱PC的中点，PA=PD=2，$BC=\frac{1}{2}AD=1$，$CD=\sqrt{3}$．