题目内容
3.现有两个盒子,第1个盒子中装有5个红球,3个黑球;第2个盒子中装有4个红球,2个黑球.现从这两个盒子中各取出1个球放在一起,再从中任取1球.求:(1)这个球是红球的概率;
(2)若发现这个球是红球,从第1个盒子中取出的球是红球的概率.
分析 (1)由已知条件利用相互独立事件概率乘法公式和互斥事件概率加法公式,能求出这个球是红球的概率.
(2)由已知条件利用条件概率计算公式能求出发现这个球是红球,从第1个盒子中取出的球是红球的概率.
解答 解:(1)∵第1个盒子中装有5个红球,3个黑球,第2个盒子中装有4个红球,2个黑球.
现从这两个盒子中各取出1个球放在一起,再从中任取1球,
∴这个球是红球的概率:
p1=$\frac{5}{8}×\frac{4}{6}+\frac{5}{8}×\frac{2}{6}×\frac{1}{2}$+$\frac{3}{8}×\frac{4}{6}×\frac{1}{2}$=$\frac{31}{48}$.
(2)发现这个球是红球,从第1个盒子中取出的球是红球的概率:
p2=$\frac{\frac{5}{8}×\frac{4}{6}+\frac{5}{8}×\frac{2}{6}×\frac{1}{2}}{\frac{31}{48}}$=$\frac{25}{31}$.
点评 本题考查概率的求法,是中档题,解题时要认真审题,注意相互独立事件概率乘法公式、互斥事件概率加法公式、条件概率公式的合理运用.

练习册系列答案
相关题目
18.对满足条件x≥0,y≥0,x+y≤2的实数x,y,记z=|x-1|+|y-1|,则z的最大值为( )
| A. | 1 | B. | 2 | C. | $\sqrt{2}$ | D. | 2$\sqrt{2}$ |
5.已知A为△ABC的一个内角,且$sinA+cosA=\frac{{\sqrt{2}}}{3}$,则△ABC的形状是( )
| A. | 锐角三角形 | B. | 钝角三角形 | C. | 直角三角形 | D. | 不确定 |
2.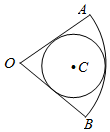 如图,圆C内切于扇形AOB,$∠AOB=\frac{π}{3}$,若向扇形AOB内随机投掷600个点,则落入圆内的点的个数估计值为( )
如图,圆C内切于扇形AOB,$∠AOB=\frac{π}{3}$,若向扇形AOB内随机投掷600个点,则落入圆内的点的个数估计值为( )
 如图,圆C内切于扇形AOB,$∠AOB=\frac{π}{3}$,若向扇形AOB内随机投掷600个点,则落入圆内的点的个数估计值为( )
如图,圆C内切于扇形AOB,$∠AOB=\frac{π}{3}$,若向扇形AOB内随机投掷600个点,则落入圆内的点的个数估计值为( )| A. | 100 | B. | 200 | C. | 400 | D. | 450 |
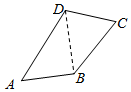 如图,已知四边形ABCD中,AB=CD=1,AD=$\sqrt{2}$BC=2,∠A+∠C=$\frac{3π}{4}$.则BD的长为$\frac{\sqrt{65}}{5}$.
如图,已知四边形ABCD中,AB=CD=1,AD=$\sqrt{2}$BC=2,∠A+∠C=$\frac{3π}{4}$.则BD的长为$\frac{\sqrt{65}}{5}$.