题目内容
14．已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1的渐近线方程为y=$±\frac{1}{3}x$，则此双曲线的离心率为（ ）| A． | $\frac{{2\sqrt{2}}}{3}$ | B． | $\frac{{\sqrt{10}}}{3}$ | C． | 3 | D． | $\sqrt{10}$ |
分析 求得双曲线的渐近线方程为y=±$\frac{b}{a}$x，由题意可得b=$\frac{1}{3}$a，由a，b，c的关系和离心率公式，计算即可得到所求值．
解答 解：双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1的渐近线方程为y=±$\frac{b}{a}$x，
由题意可得$\frac{b}{a}$=$\frac{1}{3}$，即b=$\frac{1}{3}$a，
c=$\sqrt{{a}^{2}+{b}^{2}}$=$\sqrt{{a}^{2}+\frac{{a}^{2}}{9}}$=$\frac{\sqrt{10}}{3}$a，
可得e=$\frac{c}{a}$=$\frac{\sqrt{10}}{3}$．
故选：B．
点评 本题考查双曲线的连线的求法，注意运用双曲线的方程和奖学金方程的关系，考查运算能力，属于基础题．
练习册系列答案
导学教程高中新课标系列答案
相关题目
5．已知A为△ABC的一个内角，且$sinA+cosA=\frac{{\sqrt{2}}}{3}$，则△ABC的形状是（ ）
| A． | 锐角三角形 | B． | 钝角三角形 | C． | 直角三角形 | D． | 不确定 |
2．
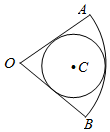如图，圆C内切于扇形AOB，$∠AOB=\frac{π}{3}$，若向扇形AOB内随机投掷600个点，则落入圆内的点的个数估计值为（ ）
如图，圆C内切于扇形AOB，$∠AOB=\frac{π}{3}$，若向扇形AOB内随机投掷600个点，则落入圆内的点的个数估计值为（ ）| A． | 100 | B． | 200 | C． | 400 | D． | 450 |
9．已知双曲线$\frac{{y}^{2}}{{a}^{2}}$-$\frac{{x}^{2}}{{b}^{2}}$=1（a＞0，b＞0）与圆x2+y2=c2（c=$\sqrt{{a}^{2}+{b}^{2}}$）交A、B、C、D四点，若四边形ABCD是正方形，则双曲线的渐近线方程为（ ）
| A． | y=±$\sqrt{1+\sqrt{2}}$x | B． | y=±$\sqrt{2}$x | C． | y=±$\frac{\sqrt{2}}{2}$x | D． | y=±$\sqrt{\sqrt{2}-1}$x |
19．与双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的一条渐近线y=$\frac{b}{a}$x的垂直的直线l交双曲线于A，B两点，若向量$\overrightarrow{OA}$+$\overrightarrow{OB}$与$\overrightarrow{m}$=（9，-$\frac{1}{3}$）平行，则双曲线C的离心率等于 （ ）
| A． | $\frac{\sqrt{10}}{3}$ | B． | $\frac{\sqrt{14}}{3}$ | C． | $\sqrt{2}$ | D． | 2 |
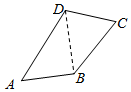如图，已知四边形ABCD中，AB=CD=1，AD=$\sqrt{2}$BC=2，∠A+∠C=$\frac{3π}{4}$．则BD的长为$\frac{\sqrt{65}}{5}$．