题目内容
13.将偶函数g(x)的图象向右平移$\frac{π}{6}$个单位,得到函数f(x)的图象,若f(x)=Asinωx(a≠0,ω>0),则ω的值可以为( )| A. | 6 | B. | 3 | C. | 4 | D. | 2 |
分析 根据三角函数图象平移关系,利用逆运算求出g(x)的集合,结合函数奇偶性的性质建立方程关系进行求解即可.
解答 解:若f(x)=Asinωx(a≠0,ω>0),向左平移$\frac{π}{6}$个单位,得到y=Asinω(x+$\frac{π}{6}$)=Asin(ωx+$\frac{π}{6}$ω),
即g(x)=Asin(ωx+$\frac{π}{6}$ω),
∵g(x)是偶函数,∴$\frac{π}{6}$ω=$\frac{π}{2}$+kπ,k∈Z,
即ω=3+6k,k∈Z,
则当k=0时,ω=3,
故选:B
点评 本题主要考查三角函数的图象和性质,根据三角函数的图象关系,进行逆运算,求出函数g(x)是解决本题的关键.

练习册系列答案
相关题目
1.设等比数列{an}的各项均为正数,且${a_1}=\frac{1}{2},{a_4}^2=4{a_2}•{a_8}$,若$\frac{1}{b_n}={log_2}{a_1}+{log_2}{a_2}+…+{log_2}{a_n}$,则数列{bn}的前10项和为( )
| A. | $-\frac{20}{11}$ | B. | $\frac{20}{11}$ | C. | $-\frac{9}{5}$ | D. | $\frac{9}{5}$ |
8.以双曲线$\frac{{x}^{2}}{3}$-y2=1的左右焦点为焦点,离心率为$\frac{1}{2}$的椭圆的标准方程为( )
| A. | $\frac{{x}^{2}}{12}$+$\frac{{y}^{2}}{16}$=1 | B. | $\frac{{x}^{2}}{12}$+$\frac{{y}^{2}}{8}$=1 | C. | $\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{12}$=1 | D. | $\frac{{x}^{2}}{8}$+$\frac{{y}^{2}}{12}$=1 |
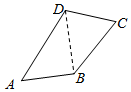 如图,已知四边形ABCD中,AB=CD=1,AD=$\sqrt{2}$BC=2,∠A+∠C=$\frac{3π}{4}$.则BD的长为$\frac{\sqrt{65}}{5}$.
如图,已知四边形ABCD中,AB=CD=1,AD=$\sqrt{2}$BC=2,∠A+∠C=$\frac{3π}{4}$.则BD的长为$\frac{\sqrt{65}}{5}$. 如图,缉私船在A处测出某走私船在方位角为45°,距离为10海里的C处,并测得走私船正沿方位角165°的方向以9海里/时的速度沿直线方向航行.我缉私船立即以v海里/时的速度沿直线方向前去截获.
如图,缉私船在A处测出某走私船在方位角为45°,距离为10海里的C处,并测得走私船正沿方位角165°的方向以9海里/时的速度沿直线方向航行.我缉私船立即以v海里/时的速度沿直线方向前去截获.