题目内容
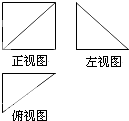 如图,某几何体的正视图是边长为2的正方形,左视图和俯视图都是直角边长为2的等腰直角三角形,则该几何体的体积等于
如图,某几何体的正视图是边长为2的正方形,左视图和俯视图都是直角边长为2的等腰直角三角形,则该几何体的体积等于考点:由三视图求面积、体积
专题:计算题,空间位置关系与距离
分析:几何体是一个四棱锥,四棱锥的底面是一个边长为2的正方形,四棱锥的一条侧棱与底面垂直,长度是2,做出四棱锥的体积.
解答:
解:由三视图知几何体是一个四棱锥,
四棱锥的底面是一个边长为2的正方形,
∴底面面积是2×2=4
四棱锥的一条侧棱与底面垂直,长度是2
∴四棱锥的体积是
×4×2=
.
故答案为:
.
四棱锥的底面是一个边长为2的正方形,
∴底面面积是2×2=4
四棱锥的一条侧棱与底面垂直,长度是2
∴四棱锥的体积是
| 1 |
| 3 |
| 8 |
| 3 |
故答案为:
| 8 |
| 3 |
点评:本题考查由三视图还原几何体并且求几何体的体积,本题解题的关键是看出这是一个底面垂直于底面的四棱锥.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
一个平面图形的面积为S,其直观图的面积为S′,则S:S′=( )
A、2
| ||
B、
| ||
| C、2 | ||
| D、1 |
已知椭圆
+
=1上一点P到椭圆的一焦点的距离为3,则P到另一焦点的距离是( )
| x2 |
| 5 |
| y2 |
| 9 |
A、2
| ||
| B、2 | ||
| C、3 | ||
| D、6 |
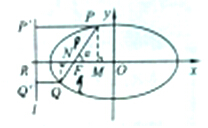 过椭圆
过椭圆