题目内容
直线l:y=k(x+2)与椭圆
+y2=1相较于A、B两点,O为坐标原点,若以OA、OB为;邻边作平行四边形OAPB.
(1)求P点的轨迹方程;
(2)是否存在直线l,使OAPB为矩形,若存在,求出k的值;若不存在,请说明理由.
| x2 |
| 2 |
(1)求P点的轨迹方程;
(2)是否存在直线l,使OAPB为矩形,若存在,求出k的值;若不存在,请说明理由.
考点:椭圆的简单性质
专题:计算题,直线与圆,圆锥曲线的定义、性质与方程
分析:(1)联立
,得:(1+2k2)x2+8k2x-2+8k2=0,由此利用韦达定理和平面向量的运算法则能求出P点的轨迹方程;
(2)假设存在直线l,使OAPB为矩形.由于OA⊥OB,则有x1x2+y1y2=0,运用韦达定理及点在直线上满足直线方程,化简整理得到k的方程,解出k,注意检验判别式是否大于0.
|
(2)假设存在直线l,使OAPB为矩形.由于OA⊥OB,则有x1x2+y1y2=0,运用韦达定理及点在直线上满足直线方程,化简整理得到k的方程,解出k,注意检验判别式是否大于0.
解答:
解:(1)联立
,
得:(1+2k2)x2+8k2x-2+8k2=0,
∵以OA、OB为邻边作平行四边形OAPB,
即有
=
+
,
设P(x,y),设A(x1,y1),B(x2,y2),
∴x1+x2=-
,
y1+y2=(kx1+2k)+(kx2+2k)=k(x1+x2)+4k=
,
∴
,∴k=-
,代入上式,得,x2+2y2+4x=0.
∴P点的轨迹方程为x2+2y2+4x=0;
(2)假设存在直线l,使OAPB为矩形.
由(1)得,x1+x2=-
,x1x2=
,
y1y2=(kx1+2k)(kx2+2k)=k2x1x2+2k2(x1+x2)+4k2
=
,
由于OA⊥OB,则有x1x2+y1y2=0,即为
+
=0,
解得,k=±
.
检验:判别式△=64k4-4(1+2k2)(8k2-2)=
>0,成立.
故存在直线l:y=±
(x+2),使OAPB为矩形.
|
得:(1+2k2)x2+8k2x-2+8k2=0,
∵以OA、OB为邻边作平行四边形OAPB,
即有
| OP |
| OA |
| OB |
设P(x,y),设A(x1,y1),B(x2,y2),
∴x1+x2=-
| 8k2 |
| 1+2k2 |
y1+y2=(kx1+2k)+(kx2+2k)=k(x1+x2)+4k=
| 4k |
| 1+2k2 |
∴
|
| x |
| 2y |
∴P点的轨迹方程为x2+2y2+4x=0;
(2)假设存在直线l,使OAPB为矩形.
由(1)得,x1+x2=-
| 8k2 |
| 1+2k2 |
| 8k2-2 |
| 1+2k2 |
y1y2=(kx1+2k)(kx2+2k)=k2x1x2+2k2(x1+x2)+4k2
=
| 2k2 |
| 1+2k2 |
由于OA⊥OB,则有x1x2+y1y2=0,即为
| 8k2-2 |
| 1+2k2 |
| 2k2 |
| 1+2k2 |
解得,k=±
| ||
| 5 |
检验:判别式△=64k4-4(1+2k2)(8k2-2)=
| 24 |
| 5 |
故存在直线l:y=±
| ||
| 5 |
点评:本题考查点的轨迹方程的求法,考查直线方程和椭圆方程联立,消去未知数,解题时要认真审题,注意韦达定理的合理运用,以及判别式大于0的条件.

练习册系列答案
 每课必练系列答案
每课必练系列答案
相关题目

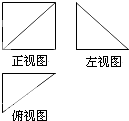 如图,某几何体的正视图是边长为2的正方形,左视图和俯视图都是直角边长为2的等腰直角三角形,则该几何体的体积等于
如图,某几何体的正视图是边长为2的正方形,左视图和俯视图都是直角边长为2的等腰直角三角形,则该几何体的体积等于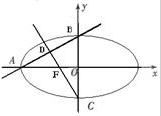 如图,椭圆
如图,椭圆