题目内容
求解析式:
(1)已知f(2x+1)=4x2+8x+3,求f(x);
(2)已知f(x+
)=x2+
-3,求f(x);
(3)已知f(x)-2f(
)=3x+2,求f(x);
(4)已知f(
+1)=x+2
,求f(x).
(1)已知f(2x+1)=4x2+8x+3,求f(x);
(2)已知f(x+
| 1 |
| x |
| 1 |
| x2 |
(3)已知f(x)-2f(
| 1 |
| x |
(4)已知f(
| x |
| x |
考点:函数解析式的求解及常用方法
专题:函数的性质及应用
分析:(1)配凑法可得f(2x+1)=(2x+1)2+2(2x+1),进而可得f(x)=x2+2x;
(2)配凑法可得f(x+
)=(x+
)2-5,进而可得f(x)=x2-5;
(3)由f(x)-2f(
)=3x+2可得f(
)-2f(x)=
+2,两式联立消去f(
)解f(x)即可;
(4)配凑法可得f(
+1)=(
+1)2-1,进而可得f(x)=x2-1,x≥1
(2)配凑法可得f(x+
| 1 |
| x |
| 1 |
| x |
(3)由f(x)-2f(
| 1 |
| x |
| 1 |
| x |
| 3 |
| x |
| 1 |
| x |
(4)配凑法可得f(
| x |
| x |
解答:
解:(1)∵f(2x+1)=4x2+8x+3
=4x2+4x+1+4x+2=(2x+1)2+2(2x+1)
∴f(x)=x2+2x;
(2)∵f(x+
)=x2+
-3
=(x+
)2-5
∴f(x)=x2-5;
(3)∵f(x)-2f(
)=3x+2,
∴f(
)-2f(x)=
+2,
两式联立消去f(
)可得f(x)=-
-x-2;
(4)∵f(
+1)=x+2
=(
+1)2-1
∴f(x)=x2-1,x≥1
=4x2+4x+1+4x+2=(2x+1)2+2(2x+1)
∴f(x)=x2+2x;
(2)∵f(x+
| 1 |
| x |
| 1 |
| x2 |
=(x+
| 1 |
| x |
∴f(x)=x2-5;
(3)∵f(x)-2f(
| 1 |
| x |
∴f(
| 1 |
| x |
| 3 |
| x |
两式联立消去f(
| 1 |
| x |
| 2 |
| x |
(4)∵f(
| x |
| x |
| x |
∴f(x)=x2-1,x≥1
点评:本题考查函数解析式的求解,属基础题.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
已知函数f(x)=x2-6x+4lnx+a(x>0),若方程f(x)=0有两个不同的实根,则实数a的值为( )
| A、a=5或a=8-4ln2 |
| B、a=5或a=8+4ln2 |
| C、a=-5或a=8-4ln2 |
| D、a=5或a=8-4ln3 |
函数y=x+
的单调减区间为( )
| 4 |
| x |
| A、(-2,0)及(0,2) |
| B、(-2,0)∪(0,2) |
| C、(0,2)及(-∞,-2) |
| D、(-2,2) |
设f(x)是定义在R上的函数,则下列叙述正确的是( )
| A、f(x)f(-x)是奇函数 | ||
B、
| ||
| C、f(x)-f(-x)是偶函数 | ||
| D、f(x)+f(-x)是偶函数 |
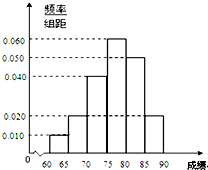 在某次综合素质测试中,共设有40个考室,每个考室30名考生.在考试结束后,统计了他们的成绩,得到如图所示的频率分布直方图.这40个考生成绩的众数
在某次综合素质测试中,共设有40个考室,每个考室30名考生.在考试结束后,统计了他们的成绩,得到如图所示的频率分布直方图.这40个考生成绩的众数