题目内容
已知
=(2,3),
=(-4,7),则向量
在
方向上设射影的数量为( )
| a |
| b |
| a |
| b |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:平面向量数量积的含义与物理意义
专题:平面向量及应用
分析:根据向量射影的定义,求出
在
方向上的射影即可.
| a |
| b |
解答:
解:根据投影的定义,得;
向量
在
方向上的射影数量是
m=|
|•cosθ=
=
=
.
故选:C.
向量
| a |
| b |
m=|
| a |
| ||||
|
|
=
| 2×(-4)+3×7 | ||
|
=
| ||
| 5 |
故选:C.
点评:本题考查了平面向量中一向量在另一向量方向上的射影的定义的应用问题,是基础题目.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知圆O1:x2+y2=1与圆O2:x2+y2-6x+8y+9=0,则两圆的位置关系为( )
| A、相交 | B、内切 | C、外切 | D、相离 |
如图,空间四边形OABC中,
=
,
=
,
=
,且OM=2MA,BN=NC,则
等于( )
| OA |
| a |
| OB |
| b |
| OC |
| c |
| MN |

A、
| ||||||||||||
B、
| ||||||||||||
C、-
| ||||||||||||
D、
|
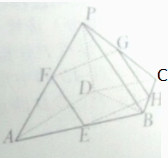 如图,在四棱锥P-ABCD中,若PD=4,DC=DB=3,PB=PC=5,AD⊥DB
如图,在四棱锥P-ABCD中,若PD=4,DC=DB=3,PB=PC=5,AD⊥DB