题目内容
已知函数f(x)=
x2-a•lnx(a∈R),g(x)=x2-2mx+4(m∈R).
(Ⅰ)若函数f(x)在x=2处的切线方程为y=x+b,求实数a与b的值;
(Ⅱ)求f(x)的单调减区间;
(Ⅲ)当a=1时,若对任意的x1∈[1,2],存在x2∈[1,2],使得f(x1)≥g(x2),求实数m的取值范围.
| 1 |
| 2 |
(Ⅰ)若函数f(x)在x=2处的切线方程为y=x+b,求实数a与b的值;
(Ⅱ)求f(x)的单调减区间;
(Ⅲ)当a=1时,若对任意的x1∈[1,2],存在x2∈[1,2],使得f(x1)≥g(x2),求实数m的取值范围.
考点:利用导数研究曲线上某点切线方程,利用导数研究函数的单调性
专题:导数的综合应用
分析:(Ⅰ)求出函数的导函数,由f′(2)=2-
=1求得a值,得到函数解析式,进一步求得f(2),由直线方程的点斜式得答案;
(Ⅱ)求出f(x)的定义域,再求出函数导函数,分a≤0,和a>0讨论求得函数的单调区间;
(Ⅲ)把对任意的x1∈[1,2],存在x2∈[1,2],使得f(x1)≥g(x2)转化为x∈[1,2]时,f(x)min≥g(x)min.然后分m<1,1≤m≤2,m>2讨论求解m的取值范围.
| a |
| 2 |
(Ⅱ)求出f(x)的定义域,再求出函数导函数,分a≤0,和a>0讨论求得函数的单调区间;
(Ⅲ)把对任意的x1∈[1,2],存在x2∈[1,2],使得f(x1)≥g(x2)转化为x∈[1,2]时,f(x)min≥g(x)min.然后分m<1,1≤m≤2,m>2讨论求解m的取值范围.
解答:
解:(Ⅰ)由f(x)=
x2-a•lnx,得f′(x)=x-
,
由f′(2)=2-
=1,得a=2,
∴f(x)=
x2-2lnx,则f(2)=2-2ln2,
即切点为(2,2-2ln2),代入方程yx+b得,b=-2ln2;
(Ⅱ)f(x)的定义域为(0,+∞),f′(x)=x-
=
,
①当a≤0时,f′(x)>0在(0,+∞)上恒成立,∴f(x)无减区间;
②当a>0时,由f′(x)<0得0<x<
,此时,f(x)减区间为(0,
);
(Ⅲ)由题意可得x∈[1,2]时,f(x)min≥g(x)min.
∵a=1时,f′(x)=x-
=
>0,f(x)在x∈[1,2]为增函数,
∴f(x)min=f(1)=
,
g(x)=x2-2mx+4=(x-m)2+4-m2.
①当m<1时,g(x)在区间[1,2]上递增,∴g(x)min=g(1)=5-2m≤
,
由5-2m≤
,解得m≥
,舍去;
②当1≤m≤2时,g(x)min=g(m)=4-m2≤
,解得m≤-
或m≥
,
∴
≤m≤2;
③当m>2时,g(x)在区间[1,2]上递减,∴g(x)min=g(2)=8-4m≤
,
由8-4m≤
,解得m≥
,∴m>2.
综上,m≥
.
| 1 |
| 2 |
| a |
| x |
由f′(2)=2-
| a |
| 2 |
∴f(x)=
| 1 |
| 2 |
即切点为(2,2-2ln2),代入方程yx+b得,b=-2ln2;
(Ⅱ)f(x)的定义域为(0,+∞),f′(x)=x-
| a |
| x |
| x2-a |
| x |
①当a≤0时,f′(x)>0在(0,+∞)上恒成立,∴f(x)无减区间;
②当a>0时,由f′(x)<0得0<x<
| a |
| a |
(Ⅲ)由题意可得x∈[1,2]时,f(x)min≥g(x)min.
∵a=1时,f′(x)=x-
| 1 |
| x |
| (x+1)(x-1) |
| x |
∴f(x)min=f(1)=
| 1 |
| 2 |
g(x)=x2-2mx+4=(x-m)2+4-m2.
①当m<1时,g(x)在区间[1,2]上递增,∴g(x)min=g(1)=5-2m≤
| 1 |
| 2 |
由5-2m≤
| 1 |
| 2 |
| 9 |
| 4 |
②当1≤m≤2时,g(x)min=g(m)=4-m2≤
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
∴
| ||
| 2 |
③当m>2时,g(x)在区间[1,2]上递减,∴g(x)min=g(2)=8-4m≤
| 1 |
| 2 |
由8-4m≤
| 1 |
| 2 |
| 15 |
| 8 |
综上,m≥
| ||
| 2 |
点评:本题考查了利用导数研究过曲线上某点处的切线方程,考查了利用导数研究函数的单调性,考查了数学转化思想方法和分类讨论的数学思想方法,是压轴题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知
=(2,3),
=(-4,7),则向量
在
方向上设射影的数量为( )
| a |
| b |
| a |
| b |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
若函数y=f-1(x+1)是定义域为R的奇函数,则函数y=f(1-2x)必过点( )
A、(
| ||
| B、(1,1) | ||
| C、(2,1) | ||
| D、(-1,1) |
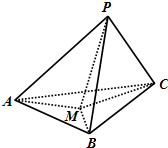 如图,在三棱锥P-ABC中,PA、PB、PC两两互相垂直,且PA=3,PB=2,PC=1,设M是底面ABC内一点,定义f(M)=(m,n,p),其中m,n,p分别是三棱锥M-PAB、三棱锥M-PBC、三棱锥M-PCA的体积,若f(M)=(
如图,在三棱锥P-ABC中,PA、PB、PC两两互相垂直,且PA=3,PB=2,PC=1,设M是底面ABC内一点,定义f(M)=(m,n,p),其中m,n,p分别是三棱锥M-PAB、三棱锥M-PBC、三棱锥M-PCA的体积,若f(M)=(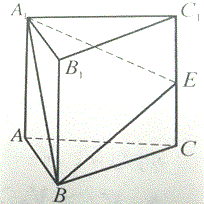 正三棱柱ABC-A1B1C1中,所有棱长都是4,E是CC1的中点.
正三棱柱ABC-A1B1C1中,所有棱长都是4,E是CC1的中点.