题目内容
8. 如图所示,为测量山高MN,选择A和另一座山的山顶C为测量观测点,从A测得M点的仰角∠MAN=60°,C点的仰角∠CAB=30°,以及∠MAC=105°,从C测得∠MCA=45°,已知山高BC=150米,则所求山高MN为150$\sqrt{6}$m.
如图所示,为测量山高MN,选择A和另一座山的山顶C为测量观测点,从A测得M点的仰角∠MAN=60°,C点的仰角∠CAB=30°,以及∠MAC=105°,从C测得∠MCA=45°,已知山高BC=150米,则所求山高MN为150$\sqrt{6}$m.
分析 由题意,通过解△ABC可先求出AC的值,解△AMC,由正弦定理可求AM的值,在RT△MNA中,AM=300$\sqrt{2}$m,∠MAN=60°,从而可求得MN的值.
解答 解:在RT△ABC中,∠CAB=30°,BC=150m,所以AC=300m.
在△AMC中,∠MAC=105°,∠MCA=45°,从而∠AMC=30°,
由正弦定理得,AM=$\frac{ACsin45°}{sin30°}$=300$\sqrt{2}$m.
在RT△MNA中,AM=300$\sqrt{2}$m,∠MAN=60°,
得MN=300$\sqrt{2}$×$\frac{\sqrt{3}}{2}$=150$\sqrt{6}$m.
故答案为150$\sqrt{6}$m.
点评 本题主要考察了正弦定理的应用,考察了解三角形的实际应用,属于中档题.

练习册系列答案
相关题目
18.若从3个海滨城市和两个内陆城市中随机选2个去旅游,那么概率是$\frac{7}{10}$的事件是( )
| A. | 至少选一个海滨城市 | B. | 恰好选一个海滨城市 | ||
| C. | 至多选一个海滨城市 | D. | 两个都选海滨城市 |
8.已知复数z1=3+ai,z2=a-3i(i为虚数单位),若z1•z2是实数,则实数a的值为( )
| A. | 0 | B. | ±3 | C. | 3 | D. | -3 |

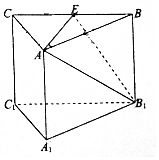 如图,在直棱柱ABC-A1B1C1中,AB=AC=4,∠BAC=90°,E为BC的中点.
如图,在直棱柱ABC-A1B1C1中,AB=AC=4,∠BAC=90°,E为BC的中点.