题目内容
3.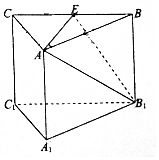 如图,在直棱柱ABC-A1B1C1中,AB=AC=4,∠BAC=90°,E为BC的中点.
如图,在直棱柱ABC-A1B1C1中,AB=AC=4,∠BAC=90°,E为BC的中点.(1)求证:平面AB1E⊥平面BCC1B1;
(2)若侧面ABB1A1为正方形,求证;BC1⊥平面AB1E.
分析 (1)利用等腰三角形的性质可证AE⊥BC,又由直棱柱的性质可证AE⊥C1C,可证AE⊥平面BCC1B1,进而证明平面AB1E⊥平面BCC1B1.
(2)以A1为原点,建立空间直角坐标系,分别求出点B1,C1,A,E,B的坐标,进而可求$\overrightarrow{B{C}_{1}}$,$\overrightarrow{{B}_{1}A}$,$\overrightarrow{{B}_{1}E}$的坐标,由$\overrightarrow{B{C}_{1}}$•$\overrightarrow{{B}_{1}A}$=0,$\overrightarrow{B{C}_{1}}$•$\overrightarrow{{B}_{1}E}$=0,可证BC1⊥B1A,BC1⊥B1E,进而利用线面垂直的判定定理即可证明BC1⊥平面AB1E.
解答 证明:(1)∵AB=AC=4,E为BC的中点.
∴AE⊥BC,
又∵在直棱柱ABC-A1B1C1中,AE⊥C1C,BC∩C1C=C,
∴AE⊥平面BCC1B1,
∵AE?平面AB1E,
∴平面AB1E⊥平面BCC1B1.
(2) 如图,以A1为原点,建立空间直角坐标系,
如图,以A1为原点,建立空间直角坐标系,
可得:B1(4,0,0),C1(0,4,0),A(0,0,4,),E(2,2,4),B(4,0,4),
可得:$\overrightarrow{B{C}_{1}}$=(-4,4,-4),$\overrightarrow{{B}_{1}A}$=(-4,0,4),$\overrightarrow{{B}_{1}E}$=(-2,2,4),
由于:$\overrightarrow{B{C}_{1}}$•$\overrightarrow{{B}_{1}A}$=16+0-16=0,
$\overrightarrow{B{C}_{1}}$•$\overrightarrow{{B}_{1}E}$=8+8-16=0,
∴BC1⊥B1A,BC1⊥B1E,
又∵B1A∩B1E=B1,
∴BC1⊥平面AB1E.
点评 本题主要考查了等腰三角形的性质,直棱柱的性质,线面垂直的判定定理,面面垂直的判定定理的应用,考查了空间想象能力和推理论证能力,属于中档题.

| A. | b<a<c | B. | a<b<c | C. | b<c<a | D. | c<b<a |
| A. | $\sqrt{3}$ | B. | 3 | C. | $2\sqrt{3}$ | D. | 6 |
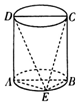
| A. | AE⊥CE | B. | BE⊥DE | C. | DE⊥CE | D. | 面ADE⊥面BCE |
| A. | (0,2) | B. | (-∞,0]∪[2,+∞) | C. | [0,2] | D. | (-∞,0]∪(2,+∞) |
| A. | 充要条件 | B. | 充分不必要条件 | ||
| C. | 必要不充分条件 | D. | 既不充分也不必要条件 |
 如图所示,为测量山高MN,选择A和另一座山的山顶C为测量观测点,从A测得M点的仰角∠MAN=60°,C点的仰角∠CAB=30°,以及∠MAC=105°,从C测得∠MCA=45°,已知山高BC=150米,则所求山高MN为150$\sqrt{6}$m.
如图所示,为测量山高MN,选择A和另一座山的山顶C为测量观测点,从A测得M点的仰角∠MAN=60°,C点的仰角∠CAB=30°,以及∠MAC=105°,从C测得∠MCA=45°,已知山高BC=150米,则所求山高MN为150$\sqrt{6}$m.