题目内容
16.分形几何学是美籍法国数学家伯努瓦B•曼德尔布罗特(Benoit B.Mandelbrot)在20世纪70年代创立的一门新学科,它的创立,为解决传统众多领域的难题提供了全新的思路.如图是按照分形的规律生长成的一个树形图,则第10行的空心圆的个数是21.
分析 可以看到第三行起每一行空心圆点的个数都是前两行空心圆点个数的和,由此可以得到一个递推关系,利用此递推关系求解即可.
解答 解:由题意及图形知不妨构造这样一个数列{an}表示空间心圆点的个数变化规律,令a1=1,a2=0,n≥3时,an=an-1+an-2,本数列中的n对应着图形中的第n行中空心圆点的个数.由此知a10即所求.
故各行中空心圆点的个数依次为1,0,1,1,2,3,5,8,13,21,34,55,89,..
a10=21,即第10行中空心圆点的个数是21
故答案为:21.
点评 本题主要考查了数列的应用,解题的关键构造这样一个数列{an}表示空间心圆点的个数变化规律,令a1=1,a2=0,n≥3时,an=an-1+an-2,属于中档题.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
4.已知F为双曲线$C:\frac{x^2}{3}-\frac{y^2}{3}=1$的一个焦点,则点F到C的一条渐近线的距离为( )
| A. | $\sqrt{3}$ | B. | 3 | C. | $2\sqrt{3}$ | D. | 6 |
1.如图,四边形ABCD是圆柱的轴截面,E是底面圆周上异于A、B的一点,则下面结论中错误的是( )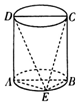

| A. | AE⊥CE | B. | BE⊥DE | C. | DE⊥CE | D. | 面ADE⊥面BCE |
15.“双曲线方程为x2-y2=3”是“双曲线离心率e=$\sqrt{2}$”的( )
| A. | 充要条件 | B. | 充分不必要条件 | ||
| C. | 必要不充分条件 | D. | 既不充分也不必要条件 |
 如图所示,为测量山高MN,选择A和另一座山的山顶C为测量观测点,从A测得M点的仰角∠MAN=60°,C点的仰角∠CAB=30°,以及∠MAC=105°,从C测得∠MCA=45°,已知山高BC=150米,则所求山高MN为150$\sqrt{6}$m.
如图所示,为测量山高MN,选择A和另一座山的山顶C为测量观测点,从A测得M点的仰角∠MAN=60°,C点的仰角∠CAB=30°,以及∠MAC=105°,从C测得∠MCA=45°,已知山高BC=150米,则所求山高MN为150$\sqrt{6}$m.