题目内容
(1)已知双曲线C:
-
=1的焦距为10,点P(2,1)在C的渐近线上,求C的方程.
(2)已知椭圆C:
+
=1(m>0,n>0)的右焦点与抛物线y2=8x的焦点相同,离心率为
,求椭圆C的方程.
| x2 |
| a2 |
| y2 |
| b2 |
(2)已知椭圆C:
| x2 |
| m2 |
| y2 |
| n2 |
| 1 |
| 2 |
考点:椭圆的标准方程,双曲线的标准方程
专题:综合题,圆锥曲线的定义、性质与方程
分析:(1)利用双曲线C:
-
=1的焦距为10,点P(2,1)在C的渐近线上,可得2c=10,
=
,求出a,b,可得双曲线的方程;
(2)求出抛物线的焦点坐标,利用椭圆右焦点与抛物线y2=8x的焦点相同,离心率为
,即可求椭圆C的方程.
| x2 |
| a2 |
| y2 |
| b2 |
| b |
| a |
| 1 |
| 2 |
(2)求出抛物线的焦点坐标,利用椭圆右焦点与抛物线y2=8x的焦点相同,离心率为
| 1 |
| 2 |
解答:
解:(1)∵双曲线C:
-
=1的焦距为10,点P(2,1)在C的渐近线上,
∴2c=10,
=
,
∴c=5,a=2
,b=
,
∴双曲线C的方程为
-
=1;
(2)抛物线y2=8x的焦点为(2,0),
∵椭圆C:
+
=1(m>0,n>0)的右焦点与抛物线y2=8x的焦点相同,离心率为
,
∴
=
,∴m=4
∴n=
=12,
∴椭圆C的方程为
+
=1.
| x2 |
| a2 |
| y2 |
| b2 |
∴2c=10,
| b |
| a |
| 1 |
| 2 |
∴c=5,a=2
| 5 |
| 5 |
∴双曲线C的方程为
| x2 |
| 20 |
| y2 |
| 5 |
(2)抛物线y2=8x的焦点为(2,0),
∵椭圆C:
| x2 |
| m2 |
| y2 |
| n2 |
| 1 |
| 2 |
∴
| 2 |
| m |
| 1 |
| 2 |
∴n=
| 42-22 |
∴椭圆C的方程为
| x2 |
| 16 |
| y2 |
| 12 |
点评:本题考查椭圆、双曲线的标准方程,考查椭圆、双曲线的几何性质,考查学生的计算能力,属于基础题.

练习册系列答案
相关题目
在等差数列{an}中,已知a1=
,a4+a5=
,若an=33,则n=( )
| 1 |
| 3 |
| 16 |
| 3 |
| A、50 | B、49 | C、48 | D、47 |
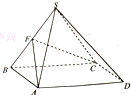 四棱锥S-ABCD,底面ABCD为平行四边形,侧面SBC⊥底面ABCD,已知∠DAB=135°,BC=2
四棱锥S-ABCD,底面ABCD为平行四边形,侧面SBC⊥底面ABCD,已知∠DAB=135°,BC=2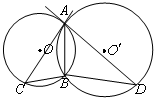 如图,⊙O和⊙O′都经过A,B两点,AC是⊙O′的切线,交⊙O于点C,AD是⊙O的切线,交⊙O′于点D,求证:AB2=BC•BD.
如图,⊙O和⊙O′都经过A,B两点,AC是⊙O′的切线,交⊙O于点C,AD是⊙O的切线,交⊙O′于点D,求证:AB2=BC•BD.