题目内容
20．圆（x-1）2+y2=1被直线$x-\sqrt{3}y=0$分成两段圆弧，则较短弧长与较长弧长之比为（ ）| A． | 1：2 | B． | 1：3 | C． | 1：4 | D． | 1：5 |
分析 根据圆的方程求得圆心坐标和半径，进而根据点到直线的距离求得圆心到直线的距离，进而分别求得较短的弧长和较长的弧长的圆心角的关系，答案可得．
解答 解：圆（x-1）2+y2=1的圆心为（1，0）到直线x-y=0的距离为$\frac{1}{\sqrt{1+3}}$=$\frac{1}{2}$，圆的半径为：1，
∴弦长为2×$\sqrt{{1}^{2}-（{\frac{1}{2}）}^{2}}$=$\sqrt{3}$．小扇形的圆心角为：120°，
∴较短弧长与较长弧长之比为1：2．
故选：A．
点评 本题主要考查了直线与圆相交的性质．在弦与半径构成的三角形中，通过解三角形求得问题的答案．
练习册系列答案
科学实验活动册系列答案
相关题目
18．在△ABC中，M是AB的中点，N是AC上一点，且$\overrightarrow{NC}$=2$\overrightarrow{AN}$，BN与CM相交于一点P．$\overrightarrow{AP}$=$λ\overrightarrow{AB}$+$μ\overrightarrow{AC}$，则λ+μ=（ ）
| A． | 1 | B． | $\frac{1}{5}$ | C． | $\frac{3}{5}$ | D． | $\frac{4}{5}$ |
8．设集合M={-1，1，2，3，4，5}，B={x|x＜3}，则M∩N=（ ）
| A． | {3，4，5} | B． | {4，5} | C． | {-1，1} | D． | {-1，1，2} |
15．已知集合A=$\left\{{\left.x\right|y=\sqrt{（{1-x}）（{x+3}）}}\right\}，B=\left\{{\left.x\right|{{log}_2}x\;≤\;1}\right\}$，则A∩B=（ ）
| A． | [-3，1] | B． | （0，1] | C． | [-3，2] | D． | （-∞，2] |
12．某公司生产一种产品，有一项质量指标为“长度”（单位：cm），该质量指标服从正态分布N（170，16）．该公司已生产10万件，为检验这批产品的质量，先从中随机抽取50件，测量发现全部介于157cm和187cm之间，得到如下频数分布表：
（Ⅰ）估计该公司已生产10万件中在[182，187]的件数；
（Ⅱ）从检测的产品在[177，187]中任意取2件，这2件产品在所有已生产的10万件产品长度排列中（从长到短），排列在前130的件数记为X．求X的分布列和数学期望．
参考数据：若X～N（μ，σ2），则P（μ-σ＜X≤μ+σ）=0.6826，P（μ-2σ＜X≤μ+2σ）=0.9544，P（μ-3σ＜ξ≤μ+3σ）=0.9974．
| 分组 | [157，162） | [162，167） | [167，172） | [172，177） | [177，182） | [182，187） |
| 频数 | 5 | 10 | 15 | 10 | 5 | 5 |
（Ⅱ）从检测的产品在[177，187]中任意取2件，这2件产品在所有已生产的10万件产品长度排列中（从长到短），排列在前130的件数记为X．求X的分布列和数学期望．
参考数据：若X～N（μ，σ2），则P（μ-σ＜X≤μ+σ）=0.6826，P（μ-2σ＜X≤μ+2σ）=0.9544，P（μ-3σ＜ξ≤μ+3σ）=0.9974．
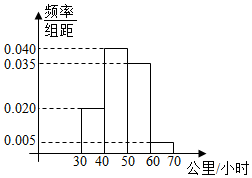某公路的一个下穿隧道限速60公里/小时，现监控了200辆经过该隧道的车速，将这200个数据作成了频率分布直方图（如图）．