题目内容
2.用数学归纳法证明:(3n+1)•7n-1(n∈N*)能被9整除.分析 先验证n=1成立,再假设n=k成立,推导n=k+1成立即可.
解答 证明:(1)当n=1时,(3+1)•71-1=27=3×9,显然能被9整除,
(2)假设n=k时,:(3k+1)•7k-1能被9整除,
那么n=k+1时,
则[3(k+1)+1]7k+1-1=(3k+1)7k+1+3•7k+1-1
=7(3k+1)7k+3•7k+1-1
=(3k+1)7k-1+6(3k+1)7k+3•7k+1,
=[(3k+1)7k-1]+(18k+27)7k,k∈N
由(3k+1)7k-1能被9整除,
(18k+27)7k能被9整除,
∴n=k+1时,(3n+1)•7n-1(n∈N*)能被9整除.
∴(3n+1)•7n-1(n∈N*)能被9整除.
点评 本题考查了数学归纳法证明,掌握数学归纳法的证明步骤是重点,由n=k到n=k+1的转化是证明关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
12.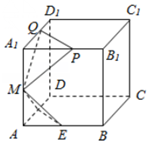 已知棱长为l的正方体ABCD-A1B1C1D1中,E,F,M分别是AB、AD、AA1的中点,又P、Q分别在线段A1B1,A1D1上,且A1P=A1Q=x,0<x<1,设面MEF∩面MPQ=l,则下列结论中不成立的是( )
已知棱长为l的正方体ABCD-A1B1C1D1中,E,F,M分别是AB、AD、AA1的中点,又P、Q分别在线段A1B1,A1D1上,且A1P=A1Q=x,0<x<1,设面MEF∩面MPQ=l,则下列结论中不成立的是( )
 已知棱长为l的正方体ABCD-A1B1C1D1中,E,F,M分别是AB、AD、AA1的中点,又P、Q分别在线段A1B1,A1D1上,且A1P=A1Q=x,0<x<1,设面MEF∩面MPQ=l,则下列结论中不成立的是( )
已知棱长为l的正方体ABCD-A1B1C1D1中,E,F,M分别是AB、AD、AA1的中点,又P、Q分别在线段A1B1,A1D1上,且A1P=A1Q=x,0<x<1,设面MEF∩面MPQ=l,则下列结论中不成立的是( )| A. | l∥面ABCD | B. | l⊥AC | ||
| C. | 面MEF与面MPQ垂直 | D. | 当x变化时,l是定直线 |
14.某区实验幼儿园对儿童记忆能力x与识图能力y进行统计分析,得到如下数据:
由表中数据,求得线性回归方程为$y=\frac{4}{5}x+a$,当江小豆同学的记忆能力为12时,预测他的识图能力为( )
| 记忆能力x | 4 | 6 | 8 | 10 |
| 识图能力y | 3 | 5 | 6 | 8 |
| A. | 9 | B. | 9.5 | C. | 10 | D. | 11.5 |
11.命题“?x∈N,x≥0”的否定是( )
| A. | ?x∈N,x<0 | B. | ?x∉N,x≥0 | C. | ?x∈N,x<0 | D. | ?x∈N,x>0 |
 在海岸A处,发现北偏东45°方向,距离A为$(\sqrt{3}-1)$海里的B处有一艘走私船,在A处北偏西75°方向,距离A为2 海里的C处有一艘缉私艇奉命以$10\sqrt{3}$海里/时的速度追截走私船,此时,走私船正以10 海里/时的速度从B处向北偏东30°方向逃窜
在海岸A处,发现北偏东45°方向,距离A为$(\sqrt{3}-1)$海里的B处有一艘走私船,在A处北偏西75°方向,距离A为2 海里的C处有一艘缉私艇奉命以$10\sqrt{3}$海里/时的速度追截走私船,此时,走私船正以10 海里/时的速度从B处向北偏东30°方向逃窜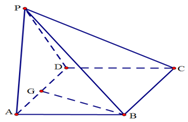 如图,四棱锥P-ABCD中,底面ABCD是∠DAB且边长为a的菱形,侧面PAD是等边三角形,且平面PAD⊥底面ABCD.
如图,四棱锥P-ABCD中,底面ABCD是∠DAB且边长为a的菱形,侧面PAD是等边三角形,且平面PAD⊥底面ABCD.