题目内容
某商人将进货单位为8元的商品按每件10元售出时，每天可销售100件，现在它采用提高销售价，减少进货量的办法增加利润．已知这种商品涨1元，其销售数就减少10个．问他将售出价定为 元时，利润获得最大．
考点：根据实际问题选择函数类型
专题：应用题,函数的性质及应用
分析：设出涨价，得到出售价及每天的销售量，由出售价减去进价乘以销售量得到一天的利润，利用配方法求最大值．
解答：
解：设涨价x元（0＜x＜10），即售出价为（10+x）元，利润为y元，依题意得：
y=（10+x-8）（100-10x）=（2+x）（100-10x）
=-10x2+80x+200=-10（x-4）2+360．
∴x=4时，ymax=360．
故当涨价x为4元，即售价为10+4=14元时每天所赚的利润最大，最大利润为360元．
故答案为：14．
y=（10+x-8）（100-10x）=（2+x）（100-10x）
=-10x2+80x+200=-10（x-4）2+360．
∴x=4时，ymax=360．
故当涨价x为4元，即售价为10+4=14元时每天所赚的利润最大，最大利润为360元．
故答案为：14．
点评：本题考查了根据实际问题选择函数模型，考查了简单的数学建模思想方法，关键是对题意的理解，是中档题．
练习册系列答案
阅读快车系列答案
相关题目
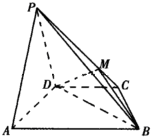在四棱锥P-ABCD中，平面PAD⊥平面ABCD，AB∥CD，在锐角△PAD中PA=PD，并且BD=2AD=8，
（几何证明选讲选做题） 如图，∠ACB=90°，AC是圆O的切线，切点为E，割线ADB过圆心O，若