题目内容
已知直线l过点P（-6，3），且它在x轴上的截距是它在y轴上的截距的3倍，求直线l的方程．
考点：直线的截距式方程
专题：直线与圆
分析：根据直线截距关系，利用待定系数法即可得到结论．
解答：
解：若直线经过原点，则设直线方程为y=kx，
∵直线l过点P（-6，3），∴3k=-6，解得k=-2，此时方程为y=-2x，
若直线不经过原点，则设方程为
+
=1，
将点P（-6，3）代入，得b=
+3=-2+3=1，
此时直线方程为
+y=1，即x+3y-3=0，
故求得直线方程是y=-2x或x+3y-3=0．
∵直线l过点P（-6，3），∴3k=-6，解得k=-2，此时方程为y=-2x，
若直线不经过原点，则设方程为
| x |
| 3b |
| y |
| b |
将点P（-6，3）代入，得b=
| -6 |
| 3 |
此时直线方程为
| x |
| 3 |
故求得直线方程是y=-2x或x+3y-3=0．
点评：本题考查直线的截距式方程，涉及分类讨论的思想，属基础题．
练习册系列答案
相关题目
在等比数列中，an＞0，且a2a7a12=729，则2a3a11=（ ）
| A、81 | B、162 |
| C、243 | D、96 |
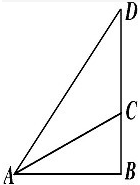已知某建筑公司在高出地面20m的小山顶建造了一座电视台CD，如图所示，设B为电视塔的正下方水平面上的点，在坡脚取一点A测得∠CAD=45°，∠CAB=α，且tanα=