题目内容
设以
=(1,-2)为方向向量的直线的倾斜角为α,则sin(2α+
)= .
| e |
| π |
| 4 |
考点:两角和与差的正弦函数,二倍角的正弦,直线的一般式方程
专题:三角函数的求值
分析:由方向向量可得tanα=-2,可得sin2α和cos2α的值,再有两角和的正弦可得.
解答:
解:∵以
=(1,-2)为方向向量的直线的倾斜角为α,
∴tanα=-2,∴sin2α=2sinαcosα=
=
=-
,
∴cos2α=cos2α-sin2α=
=
=-
,
∴sin(2α+
)=
sin2α+
cos2α=
(sin2α+cos2α)=
×(-
)=-
故答案为:-
| e |
∴tanα=-2,∴sin2α=2sinαcosα=
| 2sinαcosα |
| sin2α+cos2α |
| 2tanα |
| 1+tan2α |
| 4 |
| 5 |
∴cos2α=cos2α-sin2α=
| cos2α-sin2α |
| cos2α+sin2α |
| 1-tan2α |
| 1+tan2α |
| 3 |
| 5 |
∴sin(2α+
| π |
| 4 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| 7 |
| 5 |
7
| ||
| 10 |
故答案为:-
7
| ||
| 10 |
点评:本题考查三角函数的公式的综合应用,涉及直线的方向向量,属中档题.

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
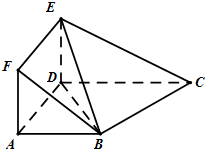 如图所示,正方形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,
如图所示,正方形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,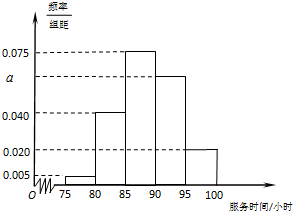 某市规定,高三毕业生三年在校期间参加不少于80小时的社区服务才合格.教育部门在全市随机抽取200位学生参加社区服务的数据为样本,按时间段[75,80),[80,85),[85,90),[90,95),[95,100](单位:小时)进行统计,其频率分布直方图如图所示.
某市规定,高三毕业生三年在校期间参加不少于80小时的社区服务才合格.教育部门在全市随机抽取200位学生参加社区服务的数据为样本,按时间段[75,80),[80,85),[85,90),[90,95),[95,100](单位:小时)进行统计,其频率分布直方图如图所示.
 在长方体中割去两个小长方体后的几何体的三视图如图所示,则切割掉的两个小长方体的体积之和等于
在长方体中割去两个小长方体后的几何体的三视图如图所示,则切割掉的两个小长方体的体积之和等于