题目内容
已知函数f(x)=
,且f(-1)=f(1)、f(-2)=f(0),
(1)求函数f(x)的解析式;
(2)若函数g(x)=f(x)-m有3个零点,求m的取值范围.
|
(1)求函数f(x)的解析式;
(2)若函数g(x)=f(x)-m有3个零点,求m的取值范围.
考点:根的存在性及根的个数判断,函数解析式的求解及常用方法
专题:计算题,作图题,函数的性质及应用
分析:(1)由题意,
,从而解出a,b;
(2)函数g(x)=f(x)-m有3个零点可化为y=f(x)与y=m有3个不同的交点,作出f(x)的图象,从而由图象可得.
|
(2)函数g(x)=f(x)-m有3个零点可化为y=f(x)与y=m有3个不同的交点,作出f(x)的图象,从而由图象可得.
解答:
解:(1)由题意,
,
解得,a=-1,b=-2;
故f(x)=
;
(2)函数g(x)=f(x)-m有3个零点可化为y=f(x)与y=m有3个不同的交点,
作f(x)的图象如下,

则由图象可知,
0<m<1.
|
解得,a=-1,b=-2;
故f(x)=
|
(2)函数g(x)=f(x)-m有3个零点可化为y=f(x)与y=m有3个不同的交点,
作f(x)的图象如下,

则由图象可知,
0<m<1.
点评:本题考查了函数解析式的求法及函数图象的作法及应用,属于中档题.

练习册系列答案
相关题目
给出下列三个命题:
①一条直线垂直于一个平面内的三条直线,则这条直线和这个平面垂直;
②一条直线与一个平面内的任何直线所成的角相等,则这条直线和这个平面垂直;
③一条直线在平面内的射影是一点,则这条直线和这个平面垂直.
其中正确的个数是( )
①一条直线垂直于一个平面内的三条直线,则这条直线和这个平面垂直;
②一条直线与一个平面内的任何直线所成的角相等,则这条直线和这个平面垂直;
③一条直线在平面内的射影是一点,则这条直线和这个平面垂直.
其中正确的个数是( )
| A、0 | B、1 | C、2 | D、3 |
当x、y满足不等式组
时,-2≤kx-y≤2恒成立,则实数k的取值范围是( )
|
| A、[-1,-1] | ||||
| B、[-2,0] | ||||
C、[-
| ||||
D、[-
|
下列图象中最左边是高青到张店71路公共汽车收支差额y与乘客量x的图象,则图①图②图③的实线所表达的实际意义是( )
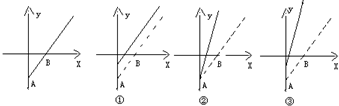

| A、①是票价不变降低成本,②是成本不变提高票价,③是降低成本提高票价 |
| B、①是成本不变提高票价,②是票价不变降低成本,③是降低成本提高票价 |
| C、①是降低成本提高票价,②是票价不变降低成本,③是票价不变降低成本 |
| D、①是成本不变提高票价,②是降低成本提高票价,③是降低成本提高票价 |
已知数列{an}满足:a1=1,an+1=2an+3(n∈N*),则a10=( )
| A、210-3 |
| B、211-3 |
| C、212-3 |
| D、213-3 |