题目内容
设集合A={x|0＜x＜2}，B={x|y=2sinx}，则A∩B=（ ）
| A、{x|1≤x＜2} |
| B、{x|0＜x＜1} |
| C、{x|0＜x≤2} |
| D、{x|0＜x＜2} |
考点：交集及其运算
专题：集合
分析：根据正弦函数的图象和性质，求出其定义域可得B，代入集合交集运算可得答案．
解答：
解：∵集合A={x|0＜x＜2}，B={x|y=2sinx}=R，
故A∩B=A={x|0＜x＜2}，
故选：D
故A∩B=A={x|0＜x＜2}，
故选：D
点评：本题考查的知识点是集合交集及其运算，难度不大，属于基础题．
练习册系列答案
相关题目
600°的终边所在的象限为（ ）
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
将参加冬季越野跑的600名选手编号为：001，002…，600．采用系统抽样方法抽取一个容量为50的样本，把编号分50组后，在第一组的001至012这12个编号中随机抽得的号码为004，这600名选手分穿着三种颜色的衣服，001到301穿红色衣服，从302到496穿白色衣服，从497到600穿黄色衣服，若从样本中任意抽取一个，则抽到穿黄色衣服的选手概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
等比数列{an}中，a3、a15是方程x2-6x+8=0的两根，则a1a9a17=（ ）
A、16
| ||||
B、-16
| ||||
C、16
| ||||
| D、64 |
如果A为锐角，且cos（π-A）=-
，那么cos（
+A）=（ ）
| 1 |
| 2 |
| π |
| 2 |
A、-
| ||||
B、
| ||||
C、-
| ||||
D、
|
若函数f（x）=sin2x-cos2x+sin2x-m在[0，
]上有零点，则实数m的取值范围为（ ）
| π |
| 4 |
A、[-1，
| ||
| B、[-1，1] | ||
C、[1，
| ||
D、[-
|
“等式lgx=5成立”是“等式lgx2=10成立”的（ ）
| A、充分条件 |
| B、必要条件 |
| C、充要条件 |
| D、既不充分又不必要条件 |
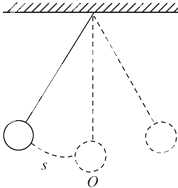如图，单摆从某点开始来回摆动，离开平衡位置O的距离s cm和时间t s的函数关系式为s=6sin（2πt+| π |
| 6 |
| A、2π s |
| B、π s |
| C、0.5 s |
| D、1 s |